Deel-3: De berekening van de planeetstanden

Menu zonder JAVA

Home

Mail

Home > Lessen > Ber3.html

Planeet-berekening

In de astrologie wordt voornamelijk met planeten gewerkt en veel minder met de sterren, alhoewel die ook zeer belangrijk kunnen zijn. Ook hieraan wordt een hoofdstuk gewijd. Onder de term "planeten" rekenen we in de astrologie ook de Zon en de Maan, hoewel deze hemellichamen in het heelal resp. een ster en een satelliet zijn. We zullen verder de Maanknoop (ook wel Draconis) en het Pars Fortuna ook maar onder de "planeten" rekenen. Alle planeten worden met de GT berekend, die u in het eerste hoofdstuk hebt leren bepalen.

Elke planeet in de efemeride wordt met een symbool aangegeven en hetzelfde symbool tekent u in op de horoskooptekening, op de plaats die bepaald is als ook alle huizen zijn berekend. 
Een overzicht van planeten en symbolen en de tekens van de dierenriem met hun symbolen treft u aan in het tabellenboekje. 
Ook in de berekeningen van de planeten wordt er van uitgegaan dat gewerkt wordt met een zgn. nul-uur-efemeride.

interpolatie

De efemeride geeft alleen de standen aan voor nul uur 's nachts en een dag later weer voor nul uur 's nachts, enzovoort.

Omdat de GT van geboorte in 99% van de gevallen niet precies nul uur is, is het noodzakelijk een berekening uit te voeren, die er tussenin ligt. We noemen dit deftig interpolatie.

Bij deze berekeningen hebben we een constante factor, die voor alle interpolaties dezelfde is, nl. de GT.

De situatie is schematisch als volgt:

In ons voorbeeld is de G.T. : 12.59.00 uur  (A)

De totale dag bestaat uit   : 24.00.00 uur  (B)

We moeten dus (A) delen door (B) om het dagdeel te vinden. Dit kan niet zomaar, aangezien uren en minuten deel uitmaken van het zestigtallig stelsel. Een simpele rekensom :

1 uur     =  3600 seconden --->

1 minuut  =    60 seconden --->

12 x 3600 = 43200 seconden

59 x   60 =  3540 seconden

Totaal    = 46740 seconden  (A)

1 dag = 24 uren --->

24 x 3600    = 86400 seconden  (B)

Nu kunt u (A) gewoon door (B) delen. Dit is : 46740/86400 = 0,5409 
Vier cijfers achter de komma is voldoende, echter wel noodzakelijk!

Berekening van de planeetstanden

Om het voorbeeld maar meteen te gebruiken, berekenen we de standen van de planeten op 16 juli 1941 met een G.T. van 12.59.00. Hieronder is een stukje efemeride ingevoegd, zodat u de standen kunt bepalen.

ZON:

Op 16 juli staat de Zon op : 23.03.41 Kreeft  (I)

Op 17 juli staat de Zon op : 24.00.56 Kreeft  (II)

De snelheid van de Zon is : 24.00.56 ofwel  23.60.56 min 23.03.41 = 0.57.15

Vermenigvuldig nu het dagdeel (0,5409) met de snelheid.

0,5409 x 00.57.15 mag niet zomaar, omdat 00.57.15  zestigtallig is.

00.57.15 moet eerst worden omgezet naar (boog)seconden. Het stukje dat de Zon aflegt in 1 dag is een klein boogje van z'n totale baan. Vandaar dat de term boogseconden wordt gebruikt. Het wordt afgekort door het teken   "  .

De berekening gaat als volgt :

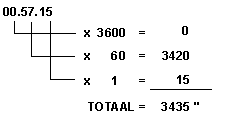
0,5409 x 3435 " = 1858 "

Dit betekent dat de Zon in "ons" dagdeel 1858 " (boogseconden) is doorgelopen. Als we deze afstand optellen bij de beginstand op 16 juli, dan krijgen we de stand voor "onze" geboortetijd.

1858 / 3600 = 0,5161 graden. Dit is 0 hele graden (°)

0,5161 x 60 = 30,9666 minuten. Dit is 30 hele minuten (')

0,9666 x 60 = 57 hele seconden (")

Zon op 16 juli (o uur) = 23.03.41  Kreeft

Bijtellen      00.30.57

               23.33.98 Kreeft

               23.34.38 Kreeft

De positie van de Zon is derhalve:

23.34.38 Kreeft.

De berekening lijkt vrij uitvoerig, maar dit komt door de twee omrekeningen.

Het principe van de planeetberekening :

• Bepaal de snelheid van de planeet:

• Zet de snelheid om in seconden;

• Vermenigvuldig met het dagdeel;

• Zet de uitkomst om naar graden,minuten,seconden;

• Tel dit op bij de eerste stand indien de planeet vooruit loopt;

• Trek dit af van de eerste stand indien de planeet achteruit loopt;

We vervolgen de berekeningen voor de Maan.

MAAN:

Op 16 juli staat de Maan op : 19.20.51 Ram    (I)

Op 17 juli staat de Maan op : 01.14.03 Stier  (II)

De snelheid van de Maan = 31.14.03 ofwel 30.73.63 min 19.20.51 = 11.53.12 graden per dag

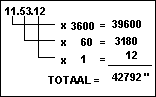
Vermenigvuldig nu het dagdeel (0,5409) met de snelheid :

0,5409 x 42792 " = 23146 "

Dit terugrekenen naar graden, minuten en seconden.

23146 /3600 = 6,4294 °  Dit is 6 hele graden.

0,4294 x 60 = 25,764 ' Dit is 25 hele minuten.

0,764 x 60 " = 45,84 " Dit is 45 hele seconden.

Tenslotte optellen bij de eerste stand van 16 juli :

Maan     =   19.20.51 Ram

Optellen     06.25.45 +  

             25.45.96      

             25.46.36 Ram

Als u in de efemeride kjkt, zult u gezien hebben, dat de standen van Zon en Maan uiterst nauwkeurig zijn opgegeven. De berekeningen zijn daardoor ook iets uitgebreider. Bij alle volgende planeetstanden staan de posities in graden en minuten vermeld. Na berekening zullen we de uitkomsten ook gaan afronden naar graden en minuten. Onze berekeningen zullen dan ook wat eenvoudiger worden.  

In de efemeride vindt u twee Maansknopen, ten eerste de Mean Maanknoop en als tweede de True Maanknoop.

We nemen in onze berekeningen altijd de Mean Maanknoop. omdat die bij de voorspellingshoroskopen het beste op datum werken. Wanneer u de gang van de Mean Maanknoop bekijkt, dan valt op dat de posities teruglopend zijn.

De Mean Maanknoop loopt dus altijd achteruit. Dit hoeft in de horoskooptekening niet speciaal aangegeven te worden, omdat dit een normale gang van zaken is.

Op 16 juli staat de Maanknoop op : 25.48 Maagd

Op 17 juli staat de Maanknoop op : 25.44 Maagd

De snelheid van de Maanknoop = 25.48 - 25.44 - = 00.04

Omzetten naar boogseconden :

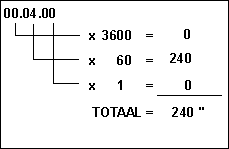
Dagdeel x snelheid :

0,5409 x 240 " = 130 "

Terugrekenen naar graden, minuten en seconden :

130 / 3600 = 0,0361 ° Dit is 0 hele graden.

0,0361 x 60 ' = 2,1666 ' Dit is 2 hele minuten.

0,1666 x 60 " = 10"

Maanknoop = 25.48.00 Maagd

Aftrekken    = 00.02.10 -

                  = 25.45.50 Maagd

Aangezien de standen slechts in graden en minuten is gegeven, zullen we het resultaat óók afronden, anders zou ons resultaat zogenaamd "nauwkeuriger" zijn dan de standen in de efemeride.

U noteert uiteindelijk voor de Maanknoop : 25.46 Maagd.

U heeft ook gezien dat we afstand die de Maanknoop in het dagdeel heeft afgelegd hebben afgetrokken van de eerste stand, aangezien de Maanknoop teruglopend is.

Wanneer een planeet teruglopend is, dan wordt dit in de efemeride aangegeven met een R op de dag van teruglopendheid. De R staat voor Retrograde. Dit verschijnsel zal in de lessen worden uitgelegd. Het retrograde-zijn van de planeten moet u wel aantekenen bij het uiteindelijke resultaat, omdat dit een grote invloed heeft op de interpretatie.

Het kan ook gebeuren dat een planeet vanuit zijn retrograde-beweging weer vooruit gaat lopen. Dit wordt dan in de efemeride aangegeven met een D op de dag, waarop dit gebeurt. De D staat voor Direct.

Uiteindelijk spreken we over ofwel direktlopende planeten of retrograde planeten.

In een zeldzaam geval vertoont de planeet totaal geen beweging. De planeet is dan Stationair. Dit kunt u aangeven met een "S" bij het eindresultaat van uw berekeningen.

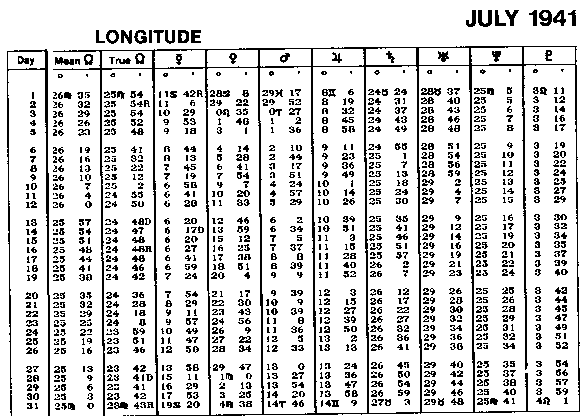
In de afgedrukte efemeride ziet u dat Mercurius vanaf 1 juli al retrograde is. Op 14 juli wordt de beweging weer direkt.

Op dezelfde wijze als voorheen berekent u de standen van de planeten Mercurius t/m Pluto. Merk op dat al deze planeten direktlopend zijn.

Tijdens de lessen kunnen een of meerdere planeetstanden als voorbeeld worden uitgerekend. Om u een controle te geven of u de berekeningen goed hebt uitgevoerd, volgt hierna een complete lijst van planeetstanden voor de opgegeven geboortetijd.

J. Ligteneigen

Naar les2

______________________________________________

Pagina voor het laatst bewerkt op / Page maintained on:   31/12/2015