tevens nieuwste nauwkeurigheden tot op 0,01"
Astrologische Artikelen door J. Ligteneigen
De
lezers weten onderhand wel hoe belangrijk de Maan is in de
progressieve horoskoop. Zij is de bevruchter van alle gebeurtenissen. Haar
gang door de zodiak sinds het geboortemoment, volgens het door ons
gehanteerde MIN-1-systeem is van wezenlijk belang voor het voorspellen van
gebeurtenissen. Zelfs een correctie op de geboortetijd is mogelijk, maar
dit vereist een grote nauwkeurigheid in de berekeningen. Wat tot voor
heden voor onmogelijk werd gehouden, kan met de huidige stand van de
rekennauwkeurigheid worden gerealiseerd.
De Maan heeft vanuit de Aarde gezien
een onregelmatige beweging. Bijna iedereen heeft de Maan wel eens voor
langere perioden gadegeslagen. Zij heeft vaak een andere kleur, meestal
veroorzaakt door atmosferische storingen, een andere vorm, soms is zij
heel groot, op andere keren is het een kleine schijf.
Ook in de astrologie staat de Maan
bekend als het veranderlijke “planeetje”. Sinds de oudheid heeft men
geprobeerd om de gang van de Maan te bestuderen en te voorspellen. Het
gebruik van de standen van de Maan werd vroeger en zelfs nu nog toegepast
bij het zaaien en oogsten van gewassen. Een nauwkeurige Maanstand is erg
belangrijk in de astrologie.
Uiteraard willen wij alle hemellichamen
zo nauwkeurig mogelijk berekend hebben. Voor bepaalde planeten is dat
redelijk eenvoudig voor elkaar te krijgen, voor andere, en daar reken ik
gemakshalve de Maan ook bij, is dit uitzonderlijk moeilijk.
De complexiteit van de Maanbeweging,
gezien vanuit de Aarde is enorm. Allereerst beweegt de Aarde zich rond de
Zon in een ellipsvormige baan. Vervolgens draait de Aarde om haar eigen
as, die ook nog eens schuin staat, volgens de formules van de ecliptica.
Tenslotte draait de Maan om de Aarde heen, ook in een ellipsvormige baan.
En of dat nog niet alles is, draait de Maan ook om haar eigen as, precies
in hetzelfde tempo als zij om de Aarde draait. Dit is er de reden van dat
de Maan altijd met hetzelfde ‘gezicht’ naar ons gericht is.
Voor astronomen is de Maanbeweging
altijd een uitdaging geweest. Ook in de tijd van Ptolemaeus werd de Maan
bestudeerd. Met een speciaal werktuig, de “Astrolabium” werden
metingen gedaan aan de standen van Zon, Maan en andere hemellichamen. Deze
metingen resulteerden in een ‘theorie’ die eeuwenlang geldig is
geweest. Later, vanaf de 16e eeuw toen de
wiskunde zijn intrede deed en met name sinds Newton zijn befaamde wetten
van de zwaartekracht formuleerde is het hard gegaan met de Maantheorie.
Belangrijke mannen als Mayer (ca.
1767), Lalande (ca. 1792), Hansen (ca. 1857), Newcomb (ca. 1878) en Brown
(ca. 1919) hebben zeer belangrijke bijdragen geleverd aan de
nauwkeurigheid van de Maanbeweging.
Wat weinigen weten is dat sinds de tabellen van Mayer de Rechte Klimming
en Declinatie van de Maan tussen 1767 en 1833 tot op 1 boogminuut
nauwkeurig werd gegeven. Vanaf 1823 werden Rechte Klimming en Declinatie a
l tot 1 boogseconde gegeven! Vanaf 1834
werden Rechte Klimming en Declinatie tot op 0,15 boogseconde berekend! De
tabellen werden in de Astronomical Ephemeris gepubliceerd en werden zelfs
om de 3 uur getabuleerd.
Je vraagt je wel eens af waarom
dergelijke nauwkeurige Maanstanden niet in een astrologische efemeride
werden afgedrukt. Gelukkig gebeurt dat tegenwoordig wel en standen tot op
1 boogseconden vinden wij in vrijwel alle moderne efemeriden genoteerd.
Sommigen tabuleren de Maanstand zelfs om 12 uur ‘s middags, zodat betere
berekeningen mogelijk zijn.
Om eens te zien hoe veranderlijk de
snelheid van de Maan is, heb ik een willekeurige efemeride gepakt en in
een maand alle standen genoteerd en vervolgens het verschil tussen alle
standen in een PC-spreadsheet ingevoerd.
|
|
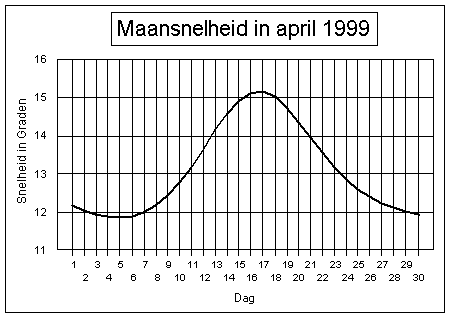
Het resultaat ziet u in bovenstaande afbeelding. Het betreft de dagsnelheden in de maand april 1999. U ziet het mooie golfpatroon, waarvan wiskundigen meteen zullen zeggen dat het een sinus-achtige curve is. In zekere zin is het dat ook, echter wel een poepje ingewikkelder. Overigens biedt het programma Newcomb-V2 u ook de mogelijkheid om grafische snelheidsverlopen per planeetn uit uw horoskoop weer te geven. Zie hiervoor de uitgebreide documentatie op de produktenpagina
Rond 5 april was de dagsnelheid net
iets minder dan 12 graden per dag, het getal waar wij gemakshalve mee
werken om heel even snel de voortbeweging van de Maan in te schatten.
Echter 12 dagen later, op 17 april is de snelheid van de Maan opgelopen
tot ruim 15 graden per dag.. Hierna neemt de snelheid weer af en begint
alles weer opnieuw. Echter dit patroon wordt niet exact herhaald, daarvoor
is de beweging te ingewikkeld.
Radix-Maan
interpolatie
Als wij de positie van de Maan in de
Radix moeten berekenen, dan gebruiken wij normaal gesproken slechts 2
datums om te interpoleren, nl. de geboortedag en de dag erna.
Interpolatie met slechts 2 standen gaat
ervan uit dat de Maan tussen deze twee standen in een rechte lijn loopt.
Dit is slechts in bepaalde situaties
zo! Als u in de afbeelding kijkt, dan is dit alleen geldig op stukken van
de baan tussen 9 en 15 april en 18 en 24 april. Dus daar waar de snelheid
vrijwel niet verandert. Op alle andere stukken verandert de
snelheid van de Maan wezenlijk, dit is zeer duidelijk tussen 15 en 18
april het geval. Twee-standen interpolatie kan u een
fout opleveren van ca. 1 boogminuut = 60 boogseconden! En dit terwijl wij
een dure efemeride hebben gekocht die de standen op de boogseconde
weergeeft.
Wij zullen ons de moeite moeten
getroosten om met iets beters te komen. Hiervoor is de 4-standen interpolatie
uit de wiskunde bedacht. Door met vier standen van de Maan te
werken, verdisconteren wij als het ware het snelheidsverloop, zoals in de
top en het dal van de snelheidsfiguur.
Over de 4-standen interpolatie is door
mij in Sagittarius 1981 nr. 6 al uitgebreid geschreven. Dit artikel zal
later ook op de website al artikel worden geplaatst.
Ik wil met u het voorbeeld van de Maan
op 16 april 1999 om 12 uur GMT eens narekenen.
Met opzet kies ik voor 12 uur GMT,
omdat deze efemeride ook voor deze tijd de Maanstand aangeeft als een
extraatje op de gebruikelijke standen voor nul uur ‘s nachts. Wij kunnen
dan meteen de twee methoden controleren op precisie.
Allereerst de twee-standen
interpolatie. Hiervoor interpoleren wij tussen 16 en 17 april. Aangezien
de GMT precies 12 uur is, is onze factor gelijk aan 12/24 = 0,50 precies.
Bij de Compact American Ephemeris staan
de standen voor GMT genoteerd in tegenstelling tot de uitgebreide American
Ephemeris, waarin de standen voor ET staan genoteerd. De ET verkrijgt u
door delta-T van het betreffende jaar op te zoeken en op te tellen bij de
GMT.
Wij werken dus met de GMT in ons
voorbeeld.
De Maanstanden zijn als volgt :
15-4:
P1 = 08.05.01 Ram
16-4
: P2 =
23.00.17
Ram
17-4
: P3
= 08.08.10 Stier
18-4
: P4
= 23.18.17 Stier
Controle : 16-4 om 12.00 uur GMT :
Maan
= 00.33.17 Stier (Volgens de
efemeride)
Eerst de twee-standen interpolatie:
Fact
= 12/24 = 0,5
P2-P1=
14.55.16
(P2-P1)
x Fact = 7.33.56
Stand = P1 + 7.33.56 = 00.34.13 Stier
U ziet meteen dat deze interpolatie
bijna 1 boogminuut afwijkt ten opzichte van de controlestand op 12 GMT,
die volgens de efemeride op 00.33.17 Stier
staat. De twee-standen interpolatie gaat geheel voorbij aan het feit dat
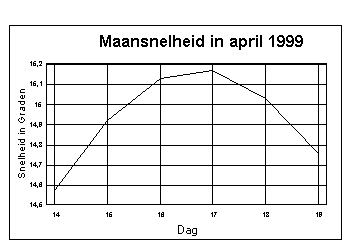
de Maan als het ware ‘afremt’. Dit kunt u mooi zien in onderstaande
afbeelding, waarbij ik een uitsnede heb gemaakt uit de voorgaande figuur.
|
|
De Maansnelheid neemt duidelijk af, echter de twee-standen interpolatie rekent met de snelheid tussen 16 en 17 april en ‘ziet’ niet dat de snelheid op 17 en 18 april al afneemt.
De vier-standen interpolatie
‘kijkt’ wel verder dan z’n neus lang is en wij zullen deze
interpolatie uitproberen.
Ik zal hierbij mijn eerder artikel uit
1981 in korte vorm samenvatten en meteen met dit voorbeeld verduidelijken.
Belangrijk is dat u nu ook de stand van
1 dag daarvoor nodig hebt!
Wij rekenen achtereenvolgens de
snelheden uit op 15, 16 en 17 april en noemen die S1, S2 en S3
S1 = P2 - P1 = 14.55.16
S2 = P3 - P2 = 15.07.53
S3 = P4 - P3 = 15.10.07
Hierna rekenen wij de versnelling uit
tussen S1/S2 en S2/S3 en noemen die V1 en V2.
V1 = S2 - S1 = 0.12.37
V2 = S3 - S2 = 0.02.14
Hierna delen wij V1 en V2 door twee en
noemen wij de uitkomst W1 en W2.
W1
= V1 / 2 = 0.06.18
W2 = V2 / 2 = 0. 01.07
Tenslotte berekenen wij het verschil
tussen W2 en W1 en delen dit door drie. De uitkomst noemen wij X1.
X1
= (W2 - W1) / 3 = -0.05.11 / 3
X1
= -0.01.44
De formule voor de juiste stand is nu:
P
=
P1 +S1 * (1+Fact) +
W1 * (1+Fact) * Fact +
X1 * (1+Fact) * Fact * (Fact-1)
* betekent vermenigvuldigen.
P
= 08.05.01 +
(08.05.01)
14.55.16 * 1,5 +
(22.22.54)
00.06.18 * 1,5 * 0,5+
(00.04.44)
-0.01.44 * 1,5*0,5*-0,5
(00.00.39)
De
totaalsom van alle waarden tussen haakjes is gelijk aan : 30.33.18 .
Dit
is gelijk aan 00.33.18 Stier
Vergelijk
dit met de controlestand in de efemeride en de afwijking is slechts 1
boogseconde!!
U
kunt zich voorstellen welke risico’s verbonden zijn aan de twee-standen
interpolatie bij een sterk veranderende Maanpositie. Bij
de planeten speelt dit effect nauwelijks een rol en de eventuele fout ligt
maximaal in de orde van zo’n 5 boogseconden, maar ook alleen in die
gevallen, waarin de snelheid aan het veranderen is. Dit
gebeurt o.a. bij de overgang van direct naar retrograde en omgekeerd.
Echter de planeetsnelheden zijn bij dergelijke overgangen zeer gering, dus
zult u er nauwelijks last van hebben.
Stelt u zich eens voor dat een
progressieve Saturnus met een snelheid van 4 boogminuten per jaar een
ingaande driehoek maakt met deze Maan. Als de Maan nu verkeerd berekend
was met een afwijking van bijna 1 boogminuut, dan hebben wij een
‘misser’, waarvan de berekende datum drie maanden verschilt met de
werkelijkheid, nl. 1 boogminuut verschil gedeeld door Saturnus’ snelheid
van 4 boogminuten maal 12 maanden.
Mocht Saturnus slechts 2 boogminuten
per jaar lopen, dan is onze ‘misser’ al bijna 6 maanden. Je zult
iemand maar een positief aspekt op datum toegezegd hebben! Wees daarom altijd op uw hoede bij
langzame progressieve planeten, die op de Radix Maan inlopen.
Hoe zit het nu eigenlijk als de Maan
progressief is?
Progressieve
Maan
We stellen ons voor dat iemand geboren
is op 1 april 1999 om 12 uur GMT precies.
Wij willen de progressieve horoskoop
opstellen voor zijn verjaardag in het jaar 2015.
Wij gaan rekenen :
2015 - 1999 = 16 .. MIN-1! = 15 dagen
na zijn geboorte.
Wij komen uit op 16 april 1999 om 12
uur GMT.
De progressieve Maan voor 1-4-2015
moeten wij interpoleren op 16 april 1999 om 12 uur GMT.
Dit hebben we al uitgebreid besproken.
De foutieve progressieve Maan voor
1-4-2015 staat op 0.34.13 Stier
met de twee-standen interpolatie.
De juiste progressieve Maan voor
1-4-2015 staat op 0.33.18 Stier
met de vier-standen interpolatie.
Voor het jaar daarop berekent u
natuurlijk ook de progressieve Maan.
De foutieve progressieve Maan voor
1-4-2016 staat op 15.43.14 Stier
De juiste
progressieve Maan voor 1-4-2016 staat op 15.43.38 Stier
Natuurlijk willen wij progressieve
aspecten gaan berekenen met deze Maan. Stel een planeet staat op precies
10 graden Leeuw en wij willen de datum van het vierkant uitrekenen.
Wij rekenen eerst met de ‘foutieve’
Maan. De snelheid van deze Maan is gelijk aan 15.43.14 - 0.34.13 =
15.09.01 graden per dag
aspect = (10.00.00 - 00.34.13) /
15.09.01 maal 365 dagen na de verjaardag = 227,18 dagen na 1-4-2015
Nu rekenen wij met de juiste Maan. De
snelheid van deze Maan is gelijk aan 15.43.38 - 00.33.18 = 15.10.19 graden
per dag.
aspect = (10.00.00. - 00.33.18) /
15.10.19 maal 365 dagen na de verjaardag = 227,22 dagen na 1-4-2015.
Wij bereiken hier dus hetzelfde
resultaat. Hoe komt dit?
De foutieve Maan wijkt ongeveer 1
boogminut af. De snelheid van de foutieve Maan is 15.09.01 en dit is
gelijk aan 15*60 + 9 = 909 minuten.
De ‘fout’ in onze berekening
bedraagt dus 1 gedeeld door 909 = 0,0011 maal 365 dagen = 0,4 dag
maximaal.
Wij zullen er met de berekening van de
progressieve-Maan aspecten er niet veel naast zitten, ondanks de kleine
afwijking in de Maanstand.
Maakt een andere planeet of
huizencusp een aspect met de progressieve Maan (dus een onderling aspect),
dan kan er weer wel een kleine (of grotere) fout in de berekende datum
sluipen.
Wees dus altijd op uw hoede bij
aspecten van de andere planeten en/of cuspen op zowel uw Radix- als
progressieve Maan.
Interpoleert u met een efemeride, gebruik dan bij voorkeur de vier-standen interpolatie.
Een
goed computerprogramma berekent de planetenstanden tot op 1 boogesonde.
Het programma Newcomb-V2 berekent de
Maanpositie tussen 1900 en 2100 met een maximale afwijking van 1,3
boogseconde.
Tussen 1950 en 2050 wordt de Maan met een maximale afwijking van 0,7
boogseconden berekend en enkele jaren rond 2000 met een maximale afwijking
van 0,5 boogseconde.
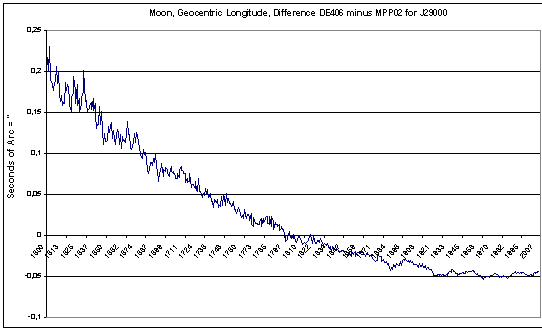
Newcomb-versie3, die ca. maart 2005 verschijnt, zal de Maan met een nog grotere precisie berekenen, zie enkele plaatjes die de nauwkeurigheid in verschillende tijdvakken weergeven.
Tussen 1200 en 1600 loopt de afwijking terug van 0,6 naar 0,2 boogseconden

Tussen 2000 en 2400 fluctueert de maximale afwijking tussen -0,05 en -0,01 boogseconden.
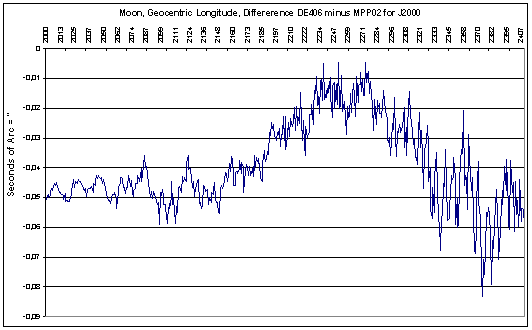
Voor de gehele tijdsperiode vanaf 1 n.Chr. tot 2800 n.Chr is het verloop van de maximale afwijking in lengte als volgt :

De afwijking van de Breedte van de Maan over deze tijdsperiode is nooit meer dan 0,1 boogseconde.
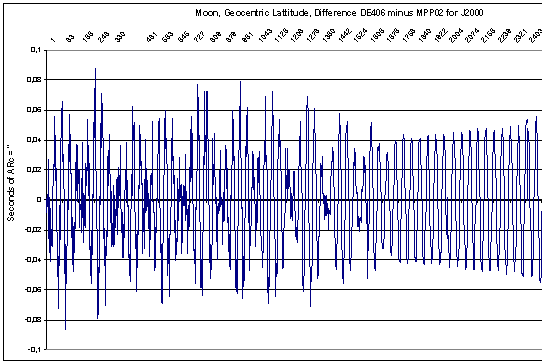
Voor bijzondere vroege perioden, 2900 v.Chr tot ca. het jaar 1 verloopt de nauwkeurigheid, zoals in de onderstaande figuur weergegeven:
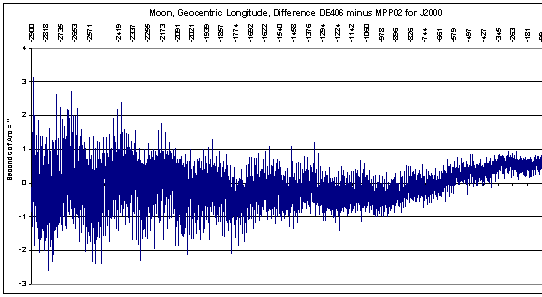
Alle vergelijkingen tussen mijn programma en de meest nauwkeurige efemeride tot op heden (de DE406 van het Jet Propulsion Laboratory) zijn in bovenstaande grafieken verwerkt.
In totaal zijn 7.000 maanstanden berekend en elke stand is vergeleken met de DE406 efemeride. Voor elke maanstand zijn 13.757 storingstermen voor de lengte berekend; 7948 storingstermen voor de breedte en 14196 storingstermen voor de afstand. In totaal dus ca. 35.900 storingstermen.
Het grote aantal storingstermen in de afstand heeft tot resultaat dat de afstand Aarde-Maan in het gunstigste tijdvak tot op 5 meter berekend kon worden!
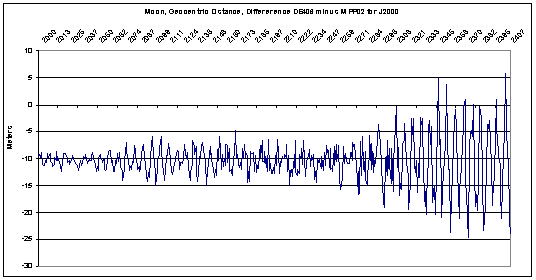
Meer informatie over de sterk toegenomen precisie van Maan en planeten zult u medio oktober 2004 op de artikelenpagina kunnen vinden.
-----
----- -----
_______________________________________________________
Pagina voor het laatst bewerkt op / Page maintained on: 31/12/2015