Astrologische Artikelen door J. Ligteneigen
In het vorige artikel werd een opgave
gegeven, die hieronder verder wordt uitgewerkt.
De opgave luidde om de nutatie voor
J2000 te berekenen, dat is 1 januari 2000 om 12.00 uur ET.
Juist voor deze datum geldt dat “T”
gelijk is aan nul, aangezien de nutatieformules gelden voor de nieuwe
Epoch J2000.
De formules voor het argument ARG
worden nu heel erg eenvoudig, nl. ARG = C in graden.
De formules voor elke term T worden nu
ook eenvoudiger en luiden nu als volgt:
Term
= A x sin(ARG)
We starten met de nutatie in lengte :
1 januari 2000, 12h ET
JD = 2451545,0
T=0
Term-1:
C=125,0446.
ARG = 125,0446°
sin(ARG)
= 0,818705
A
= -17,1996”
Term
= -17,1996 x 0,818705 = -14,0814
Term-2:
C
= 200,9329. ARG = 200,9329°
sin(ARG)
= -0,35727
A
= -1,3187
Term = -1,3187 x -0,35727 = 0,4711
Op soortgelijke wijze berekent u alle
termen, waarvan hieronder de resultaten:
T1 = -14,0814
T2 = 0,4711
T3 = -0,2212
T4 = -0,1939
T5 = -0,0061
T6 = 0,0504
T7 = 0,0142
T8 = 0,0289
T9 = 0,0158
T10 = -0,0086
T11 = 0,0155
T12 = 0,0125
T13
= -0,0105
Totaal =
-13,913” in lengte.
De
nutatie volgens alle 106 termen van Woolard bedraagt -13,9677”.
Ons
verschil bedraagt 0,054” en is precies voldoende om een planeten
nauwkeurigheid van 0,5” te waarborgen, vooropgesteld dat we de planeten
tot op 0,5” nauwkeurig kunnen berekenen.
Voorlopig
is dit ruim voldoende.
Wij
vervolgen met de nutatie in de ecliptica.
Let
u erop dat nu de cosinus genomen moet worden.
Term-1:
C = 125,0446. ARG = 125,0446°.
cos(ARG) = -0,5742
A = 9,2025
Term = 9,2025 x -0,5742 = -5,2842
Term-2:
C = 200,9329. ARG = 200,9329°.
cos(ARG) = -0,9340
A = 0,57359
Term = -0,9340 x 0,57359 = -0,5357
Alle
termen zijn:
T1 = -5,2842
T2 = -0,5357
T3 = 0,0226
T4 = 0,0305
T7 = -0,0215
T8 = 0,0133
T9
= -0,0109
Totaal =
-5,7861” in ecliptica.
Deze
waarde telt u op bij de theoretisch berekende ecliptica.
De waarde,
berekend met de 55 termen van Woolard levert -5,7671” op.
Het verschil is 0,019” en is
voldoende klein om een goede ecliptica te kunnen berekenen.
Hiermee sluiten we het artikel over de
nutatie af.
========================= GMT
versus UT =============================
Sinds oudsher wordt in de astrologie
het begrip Greenwichtijd Mean Time,
ofwel GMT gehanteerd
Deze komt tot stand door de tijdsoort
van de geboortetijd af te trekken (voor Oosterlengte) of bij te tellen
(voor Westerlengte).
Deels is het gebruik van de GMT als
begrip terug te voeren op historische cq. traditionele overwegingen. In
alle oudere boeken wordt de GMT gehanteerd. Astrologie is nu eenmaal een wetenschap, waarin nog erg veel traditie is terug te vinden.
Anderzijds komt dit door een gebrek aan
flexibiliteit om mee te gaan met de nieuwe ontwikkelingen op astronomisch
gebied. Astrologen zijn nu eenmaal geen astronomen! Bovendien is het
makkelijk om te blijven praten in “oude” termen.
Voorlopig kan het ook helemaal geen
kwaad als u de term GMT gebruikt.
Het is desalniettemin interessant eens
te kijken naar het begrip UT als vervanging van de GMT.
U.T.:
Universal Time
Sinds de introductie van de kwartsklok
eind jaren dertig, die een enorme precisie kent, kunnen de astronomen de
rotatie van de Aarde om haar as bijzonder nauwkeurig bepalen. Daarbij is
vast komen te staan dat de Aarde niet met een constante snelheid
ronddraait, maar dat er fluctuaties zijn.
Enerzijds zijn dit periodieke,
seizoensgebonden fluctuaties (zoals de verplaatsing van water- en
luchtmassa’s). Anderzijds zijn er ook schommelingen, die niet vooruit
zijn te bepalen, maar samenhangen met o.a. de zonne-activiteit en de
getijdenbeweging in de zeeën en oceanen.
De Universal Time, die dus wordt beïnvloed
door deze schommelingen, wordt de UT1
genoemd.
In ons dagelijks leven wordt niet deze
UT1 gebruikt, omdat deze te onzuiver is voor diverse toepassingen. In
plaats hiervan wordt de UTC
gebruikt, De Coordinated Universal
Time.
Deze UTC wordt met behulp van een
cesium atoomklok bijgehouden en heeft een precisie van 1 nanoseconde per
dag, dat is 0,000 000 001 sec.
In diverse laboratoria in de wereld
wordt de precisie van deze UTC bewaakt Deze nauwkeurige tijd werd vele
jaren doorgegeven aan een instantie, die in 1912 werd opgericht: het
Bureau International de l’Heure. Dit bureau kreeg als taak de
tijdmetingen op de diverse sterrenwachten te coördineren.
Tegenwoordig wordt deze coördinatie
gedaan door de International Earth Rotation Service (IERS). De atoomtijd
wordt tegenwoordig berekend door het Bureau International des Poids et
Mesures (BIPM).
De UTC loopt dus werkelijk constant aan
de hand van de atoomtijd, terwijl de UT1 die afhankelijk is van de
Aardrotatie regelmatig hiervan afwijkt.
Het blijkt dat de Aarde continu
langzamer gaat draaien. Hierdoor wordt de dag steeds langer. Om die reden
is het noodzakelijk om af en toe een schrikkel-seconde in te lassen, zodat
de UTC en de UT1 weer min of meer gelijk lopen.
Hoe
wordt nu de UT1 bepaald?
Op diverse sterrenwachten in de wereld
zijn er speciale instrumenten, waarmee zgn. “doorgangstijdstippen” van
hemellichamen kunnen worden gemeten. Een van die instrumenten is een Zeiss
Ni2 pendulum astrolabium. Met behulp van dit instrument wordt de tijd
gemeten waarop een bepaalde ster een bepaalde zenit-afstand heeft bereikt.
Door deze waarnemingen te doen aan verschillende sterren over de gehele
reeks, kan men de geografische lengte en breedte van de waarnemingsplaats
berekenen.
Uit die gegevens kan worden bepaald wat
het verschil tussen UT1 en UTC is.
Dit betekent tevens dat de
sterrenwachten ook over nauwkeurige klokken dienen te beschikken, anders
kunnen de exacte doorgangstijdstippen niet worden bepaald.
Ten behoeve van de navigatie overal op
Aarde wordt het verschil tussen UT1 en UTC door diverse zenders
uitgezonden op de korte- en lange golf. Hiertoe worden enorme eisen
gesteld, om dit verschil tussen UT1 en UTC “op tijd” aan te laten
komen.
Internationaal zijn er afspraken
gemaakt dat het vrschil tussen UT1 en UTC niet meer dan 0,9 seconde mag
bedragen. Op het moment dat dit dreigt te gebeuren, wordt een
schrikkelseconde ingelast. Dit gebeurt niet zomaar, maar op vastgestelde
datums, meestal in juni en december.
Hiervan lezen we dan wel eens iets in
de krant.
Welke
gevolgen heeft dit voor de berekening van de horoskoop?
In de loop der jaren hebben al die
schrikkelsecondes zich behoorlijk opgestapeld en nu zitten wij al met een
verschil tusen UT1 en UTC van 61 seconden. Als u kijkt naar de afgedrukte
efemeride in Sagittarius Nr. 1 van dit jaar (blz. 12), dan ziet u onderaan
staan: “Delta-T” is 61 seconden.
Dat is erg veel. Het betekent dat de
Aarde 61 seconden langzamer draaide dan volgens de volkomen regelmaat
verwacht kon worden.
Dit houdt tevens in dat de planeten
(wanneer zij rechtlopend zouden zijn) qua lengte verder in hun baan t.o.v.
de Aarde staan.
Omdat astronomen deze gevolgen al lang
in de gaten hadden, is er een universele tijdsoort ingesteld om de
planeten te berekenen, de zgn. Efemeride
Tijd, kortweg ET genoemd.
E.T.:
Efemeride Tijd
Reden om de ET in te voeren zijn
voortgekomen uit een uitvorige studie door Spencer Jones (1939)1,
waarna Clemence (1948)2 het begrip ET heeft geïntorduceerd.
In 1984 hebben Stephenson en Morrison3
een bijzonder uitvoerige studie gepresenteerd op basis van 50.000 timings
van sterbedekkingen door de
Maan over een periode van 2700 jaar.
Hieruit zijn formules ontstaan, die
Delta-T kunnen berekenen over een lange periode.
In de grafiek
hieronder ziet u de
waarden van Delta-T vanaf 1900,5 t/m 2002. Zoals u kunt zien, is Delta-T
niet altijd positief. In de jaren tussen 1850 en 1950 is Delta-T rgelmatig
kleiner dan nul geweest, d.w.z. daar draaide de Aarde sneller dan volgens
het perfecte regelmatige patroon.
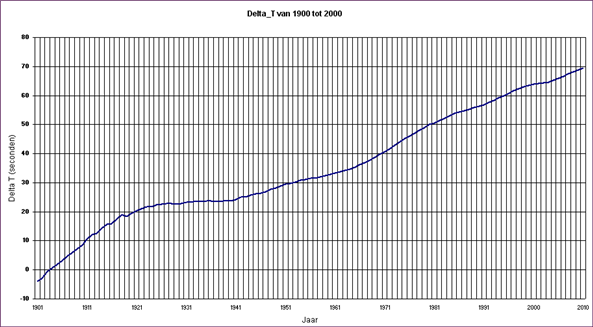
De waarden van Delta-T zijn te halen uit
de American Ephemeris. Hierin staat een tabel, die meestal begint vanaf
1860 tot op het jaar waarin de efemeride is gemaakt. Dit komt omdat Delta-T niet is te
voorspellen. Het hangt er helemaal vanaf wat er in een bepaald jaar
gebeurt met de Aardrotatie. Deze tabellen kunnen dus alleen achteraf
gemaakt worden.
In een computerprogramma kan Delta-T
voor elk jaar in een tabel worden gezet, waaruit het programma dan voor een
bepaalde datum Delta-T kan halen. Echter de meeste gepubliceerde tabellen
lopen vanaf 1800 tot op heden.
In het Explanatory Supplement to the
Astronomical Ephemeris4 staan tussen 1621 en 1821 af en toe
waarden gepubliceerd en vanaf 1821 tot 1972 voor elk jaar de exacte waarde
van Delta-T tot op 0,01 seconde nauwkeurig.
Naar aanleiding van het uitgebreide
onderzoek van Stephenson en Morrison zijn verschillende formules gemaakt,
die elk een specifiek tijdvak afdekken. Hierbij kan bij een bepaalde
waarde van “T” (de Juliaanse Eeuw) Delta-T worden berekend.
Schmadel en Zech6 hebben
drie formules gemaakt, waarbij Delta-T voor de periode 1800-1988 kan
worden berekend, elk met een eigen precisie.
Hoe korter de periode (de time-span),
hoe nauwkeuriger de formule.
|
Delta-T
= -0,00002 + 0,000297.T + 0,025184.T2 - 0,181133.T3
+0,553040.T4 - 0,861938.T5
+
0,677066.T6 - 0,212591.T7 |
De bovenstaande formule, geldig van 1900 tot 1988 geeft Delta-T in dagen. Om Delta-T in seconden te krijgen, dient u de uitkomst met 86400 te vermenigvuldigen.
De Juliaanse Eeuw “T” geldt voor de
Epoch J1900 (31 dec. 1899, 12H UT).
Deze formule is alleen geldig tussen
1900 en 1988 en heeft in dit bereik een gemiddelde nauwkeurigheid van ca.
0,5 seconde met een maximumfout van tussen 1 en 1,5 seconde. Dit komt 12
keer voor in de periode 1900-1988.
Een grafiek van deze afwijkingen ziet u
hieronder afgebeeld. De uitkomsten van de formule zijn
vergeleken met de nauwkeurige tabel in het Explanatory Supplement.
De balkjes die omhoog gaan, geven aan
dat de formule Delta-T te hoog heeft berekend. De balkjes die naar beneden
gaan, geven aan dat Detla-T volgens de formule minder is dan de
nauwkeurige tabel uit het Explanatory Supplement.
Over een zeer groot deel van het bereik
blijft de nauwkeurigheid van Delta-T tussen de -1 en +1 seconde, waarmee
een goede nauwkeurigheid voor uw planetenberekening is gewaarborgd.
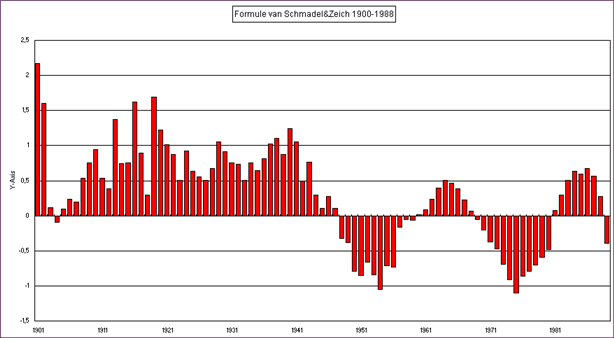
Ik gebruik deze formule zelf ook in mijn eigen programma’s. Pas wanneer mijn planetenformules heel erg nauwkeurig worden (onder de 0,1 boogseconde) dan zal ik toch de nauwkeurige tabel moeten gebruiken, maar voorlopig voldoet dit prima voor ons huidige doel.
Hoe
zit het dan met de jaren tussen 1988 en heden?
Als u de waarden van Delta-T in dit
tijdvak grafisch uitzet, dan blijkt Delta-T in een vrijwel rechte lijn
door te lopen.
Hiervoor kan met een eenvoudige formule
worden volstaan, die hieronder gegeven wordt en is bepaald met behulp van
lineaire regressie met een verwachte fout van max. 1 seconde.
De formule is uitlsuitend geldig tussen
1988 en 2010, ofwel waarden van “T” tussen 0,88 en 1,10.
|
Delta-T
= -23,675 + 89,1601.T |
Bedenkt u hierbij wel dat de waarden
tussen 2000 en 2010 ingeschat zijn. Alleen de toekomst zal uitwijzen wat
de werkelijke afwijkingen zijn.
Planetenberekening met
E.T.
Als u de planeten gaat berekenen met
een efemeride, dan dient u heel goed te letten op de aanwijzingen bij de
efemeride. In het voorwoord staat altijd of u bij de UT (de oude GMT)
delta-T moet optellen of dat de efemeride dat alvast voor u gedaan heeft.
Efemeriden die recentelijk gedrukt zijn
over de periode 1900-2000 kennen de waarden van Delta-T al, dus die wordt
zeer waarschijnlijk verwerkt in de kolom UT/GMT.
Efemeriden die werkelijk vooruit
gedrukt worden (bijvoorbeeld de periode 2000-2050) kennen Delta-T
natuurlijk nog niet en daar moet u Delta-T zelf uitrekenen en optellen bij
de UT/GMT.
Ook de Delta-T waarden in de American
Ephemeris 2000-2050 zijn ingeschat!
Nieuwe
ontwikkelingen
Het begrip ET bestaat al weer enige
tijd en is langzamerhand verouderd.
ET werd geïntroduceerd vóór de grote
ontwikkelingen in de relativiteitstheorie. De ET wordt hoofdzakelijk
gebruikt voor de berekening van geocentrische efemeriden, dus de standen
van de hemellichamen bekeken vanaf de Aarde. Onze
astrologische/astronomische berekeningen zijn geocentrisch, dus wij kunnen
met het begrip ET gewoon door blijven gaan.
De basis van de ET is de ET-seconde,
die is afgeleid van de lengte van het tropisch jaar in 1900.
Tegenwoordig spreken de astronomen van TDT
(Terrestrial Dynamical Time), die in 1977 werd geïntroduceerd en
waarvan de basis de SI-seconde is, gebaseerd op de trillingen van het
Cesiumatoom.
Voor berekeningen, die gebaseerd moeten
zijn op het zwaartepunt van het zonnestelsel (let op: dat is niet altijd
precies het middelpunt van de Zon!) werd het begrip TDB
(Barycentric Dynamical Time) gebruikt. Zeer veel uiterst precies
astronmische berekeningen worden nl. gedaan voor het barycentrum, dat is
het zwaartepunt van het zonnestelsel op enig moment. Uiteraard moet je dan
precies weten waar alle hemellichamen staan om het zwaartepunt te kunnen
bepalen.
Er zijn reeksen ontwikkeld om de TDT
(gelijk aan de ET) te kunnen omrekenen naar TDB, waarin de standen van de
hemellichamen zijn verdisconteerd. Dergelijke reeksen leveren een TDB op
met een nauwkeurigheid van ongeveer 1 nanoseconde (0,000 000 001)
Om maar even aan te geven met welke
precisie er tegenwoordig in de astronomie wordt gewerkt.
In de volgende aflevering ga ik nog
even in op Delta-T en geef u enkele formules, die u kunt gebruiken voor de
jaren vanaf 2000 v.Chr, gebaseerd op de gegevens van Stephenson en
Morrison.
Literatuur:
1.
Spencer Jones, H., 1939,
Monthly Notices of the Royal Astron. Society, 99,
541;
2.
Clemence, G.M., 1948,
Astronomical Journal, 57, 125;
3.
Stephenson,F., Morrison, L.V.,
1984, Philos. Trans. R. Soc. London Ser. A 313,
47.;
4.
Explanatory Supplement to
the Astronomical Ephemeris and the American Ephemeris
and Nautical Almanac,
1977, 90;
5.
Schmadel, L.D., Zech, G.,
“Empirical transformations from UT
tot ET for the period
1800-1988”, Astronomische Nachtrichten, 1988, 309,
219-221;
______________________________________________
Pagina voor het laatst bewerkt op / Page maintained on: 31/12/2015