Astrologische Artikelen door J. Ligteneigen
Wat
is sterrentijd?
Voor een korte uitleg van het begrip
Sterrentijd, verwijs ik naar afb.1 hieronder. Stelt u zich voor dat de
Aarde zich in een baan om de Zon heen beweegt. Op zich niets vreemd, dit
is de realiteit.
|
|
De verhoudingen in de tekening zijn met
opzet veranderd om het verhaal beter tot zijn recht te laten komen.
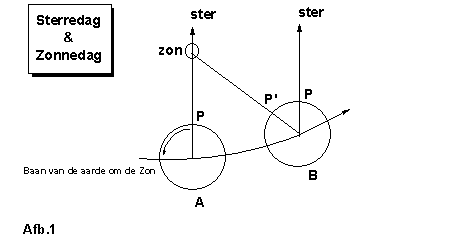
De baan van de Aarde om de Zon is
aangegeven met een kromme pijl. Op een bepaalde dag staat de Aarde in
positie “A”. Iemand kijkt vanuit een punt “P” naar een ver
afgelegen Vaste Ster.
Een dag later is de Aarde aangekomen in
positie “B”. De waarnemer kijkt op precies dezelfde plaats weer naar
de Vaste Ster in punt “P”.
De tijd, die de Aarde nodig had om
precies 1 maal rond zijn as te draaien is de Sterrentijd. Deze bedraagt 23
uur 56 minuten en 3,45
seconden.
De waarnemer in positie “B” die
zojuist de Vaste Ster in punt “P” observeerde, zal een kleine tijd
later de Zon kunnen observeren in punt P’. De Aarde is dan een klein
beetje verder gedraaid om zijn as, waardoor punt “P” is doorgedraaid
naar punt P’. Dit punt P’ wordt vanaf P ongeveer 3 minuten en 56,55
seconden later bereikt.
In de astronomie wordt voor de
vaststelling van de sterrentijd niet naar een ver weg liggende Vaste Ster
gekeken, maar naar de passage van het lentepunt over de meridiaan “P”.
Het grappige is dat het lentepunt in de hemel als zodanig niet
waarneembaar is. De stand van de Zon is dat echter wel en de precieze
lengte van de Zon is tevens de afstand vanaf datzelfde lentepunt. Herinner
dat het lentepunt hetzelfde is als het punt NUL graden Ram. Vanaf hier
worden alle hemellichamen in lengte bepaald.
De meridiaan “P” is de positie van
een waarnemingspunt “P” op Aarde, precies gericht op het Zuiden.
Per definitie geldt : bij de passage
van het lentepunt over de meridiaan is de sterrentijd altijd precies 0h00m00s.
De sterrentijd zegt dus iets over de
tijd die is verstreken sinds de passage van het lentepunt over de
meridiaan. En die meridiaan kan elke plaats op Aarde zijn, zoals uw
geboorteplaats.
Als bijvoorbeeld de sterrentijd in uw
horoskoop precies 2.00.00 uur is, dan wil dit zeggen dat het lentepunt 2
uur geleden over het exacte Zuiden is gegaan, richting het Westen.
Onderstaande schets maakt dit nog even duidelijk:
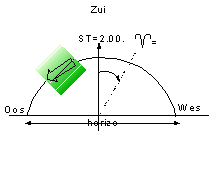
U kijkt als het ware naar het Zuiden
vanuit uw waarnemingsplaats. Pal op het Zuiden stond 2 uur geleden het
lentepunt, aangegeven door .
De grote pijl geeft de draaiing van de Aarde aan, richting het Oosten.
Door deze draairichting lijkt alles naar het Westen te draaien en bij het
Westen onder te gaan. U ziet het lentepunt dus al in een boog naar het
Westen toe draaien. Als de Aarde nog 4 uur verder is gedraaid, dan zou het
lentepunt pal in het Westen onder de horizon verdwijnen. De “klok” van
iedere horoskoop wordt aangegeven door de Sterrentijd. Die bepaalt waar
het punt zich bevindt, maar tevens bepaalt die
klok het exacte Zuiden (het MC). Het is dan verder afhankelijk van de
breedte van de plaats waar de Ascendant komt te liggen en alle andere
huizen, maar dit is een ander verhaal.
Een sterrendag
is de tijd, die de Aarde nodig heeft om precies 1 maal om zijn as te
draaien (23h56m3,45s). Een sterrendag is
dus net iets korter dan een gewone (middelbare) zonnedag.
Een (middelbare) zonnedag is de tijd die de Aarde nodig heeft om een waarnemer de Zon
steeds weer in punt P’ te laten waarnemen.
De dagen in de efemeriden zijn
middelbare zonnedagen van precies 24 uur. In 1 middelbare zonnedag is de
Aarde eenmaal om zijn as gedraaid plus nog een klein beetje van P naar
P’. In de kolom Sterrentijd (Sidereal Time) ziet u voor elke volgende
dag de Sterrentijd (hierna ST genoemd) genoteerd staan. Als u eens
narekent hoeveel de ST per dag toeneemt, dan komt u op vrijwel dezelfde
waarde uit als ik eerder genoemd heb: 3m56,555s. In
Sagittarius-1999 nr.3 heb ik voor de maand mei 17 keer 3m57s
geteld en 13 keer 3m56s.Dit levert een gemiddelde op
van 3m56,5666s en dit is vrijwel precies de waarde
die het moet zijn.
Theoretische
berekening van de ST
Het is juist interessant om nu zelf de
waarde van de ST te berekenen voor een willekeurige dag en tijd. Hiermee
kunt u dan de huizen van de horoskoop zonder huizentabel berekenen (indien
u ook de formules heeft voor de Placidus huizenberekening).
Sinds jaar en dag gebruik(te) ik de
volgende formule voor de ST:
Mean Sidereal Time, MST = 99,6909833o +
36000,7689oT + 0,00038708o T2
De epoch voor deze formule is J1900.
De formule geeft de ST in graden bij
een gegeven waarde van T (de Juliaanse Eeuw). T moet gebaseerd zijn
op de UT en niet op de ET! De Sterrentijd in uren krijgt u door de
uitkomst te delen door 15.
Wij zullen de formule met een voorbeeld
uittesten. Ik gebruik de Complete Planetary Ephemeris bij dit voorbeeld
die de ST tot op 0,1 seconde precies weergeeft.
Datum: 13 november 1978, 0 uur UT (dit
is de oude GMT).
Juliaanse Datum = 2443825,5
Juliaanse Eeuw = T = 0,7886516085
T2 = 0,6219713588
Herinner dat u de waarde van T en T2
met 10 cijfers achter de komma bewaart.
ST = 99,6909833 + 28392,06428 +
0,000240752 = 28491,7555 graden.
De uitkomst delen door 15 om het aantal
uren te krijgen. Dit geeft 1899,450367 uren. Dit is eigenlijk al de ST,
maar die moet u nog omzetten tussen nul en 24 uur. Daarom deelt u de
uitkomst door 24.
Dit wordt dan 79,14376529.
Dit zijn dus 79 hele dagen. Die haalt u
weg. Er blijft dan over: 0,14376529 dag. Vervolgens vermenigvuldigt u dit
met 24 en u krijgt :
MST = 3,45036696 = 3h27m01,32s.
Er is echter nog een toevoeging nodig
op de MST om de werkelijke ST te krijgen. Ook hier moeten wij rekening
houden met de nutatie
in lengte, waarover in de vorige aflevering al het nodige is
geschreven. Onder invloed van de nutatie krijgt de aardas een duw- en
trekbeweging te verwerken, die voornamelijk door de Zon en Maan wordt beïnvloed.
Ik herhaal hier nog even de formule van
de twee belangrijkste termen, die afhankelijk zijn van de lengte van de
Draconis:
NUT
(lengte) = -17,23" x sin(DR) + 0,21"x sin(2 x DR)
Wij moeten dus de Draconis berekenen,
zoals in deel-3 is uitgelegd. Hierna kunnen wij bovenstaande formule
uitrekenen.
Draconis(DR)
= 173,82025 = 23049’12”
Maagd.
sin(DR) = 0,107648
2 DR= 347,6405
sin(2 DR) = -0,214044
NUT (lengte) = -17,23 x 0,107648 +
0,21 x -0,214044 = -1,90”
Ik herinner er nogmaals aan dat er hier
slechts 2 termen zijn gegeven voor de berekening van de nutatie. Alle
andere termen moeten eigenlijk ook worden berekend.
Hierdoor komt de
werkelijke NUT (lengte) uit op -3,373”.
De uiteindelijke ST (ook wel Apparent
Sidereal Time genoemd) wordt gegeven door de volgende formule:
STAPP
= MST + NUT x cos(ecliptica)/15
Hierbij moet dus ook de ecliptica
worden berekend, volgens de formules in Deel-2 van deze serie.
De
ecliptica = 23,4420395
cos(ecliptica)
= 0,91746
AST = 3h27m01,32s
+ (-3,373”) x 0,91746/15 = 3h27m01,32s
- 0,21s =
3h27m01,11s
De
Complete Planetary Ephemeris geeft : AST = 3h 27m
01,1s
Onze afwijking is slechts 0,01 seconde
in Sterretijd!!
Dit resultaat kon alleen maar bereikt
worden, omdat de nutatie van -3,373” zo precies gegeven werd.
Had u in plaats hiervan de (veel
onnauwkeuriger) waarde -1,90” gebruikt, dan was de AST als volgt
geweest:
AST = 3h27m01,32s
+ (-1,90”) x 0,91746/15 = 3h27m01,32s -
0,12” =
3h27m01,20s
De afwijking bedraagt dan 0,1 seconde
in Sterretijd, toch nog redelijk in de buurt van de werkelijke waarde.
U mag de nutatie
in lengte nooit vergeten, want de aardas staat nu eenmaal onder invloed
van Zon, Maan en planeten, die er allemaal hun aantrekkingskracht op
uitoefenen.
In Sagittarius wordt elke keer een
bladzijde van de Compact American Ephemeris afgedrukt. Hierop vindt u de
AST terug, echter op de hele seconde afgerond. Dat is jammer, want als u
weet dat elke seconde sterrentijd ca. 15 boogseconden in de huizenpositie
uitmaakt, dan kunt u uw conclusies trekken.
Bij een snelrijzende Ascendant (Vissen
op onze Noorderbreedte) kan 1 seconde sterrentijd zelfs 40 boogseconden
uitmaken in de Ascendantsgraad.
Een afwijking van 0,1 seconde
sterrentijd is dan altijd nog 4 boogseconden in de Ascendant!!
Wij moeten dus naar iets beters toe.
Niet van mij hoor! Ik bedoel eigenlijk dat de astronomie iets beters kan
bieden.
Lees en huiver.....
De tot nu toe gebruikte formule voor de
Mean Sidereal Time is te vinden in het Explanatory Supplement1.
Tijdens mijn onderzoek naar de nutatie
stuitte ik per toeval op een artikel van P. Bretagnon2, waarin
een uitzonderlijk precieze formule voor de sterrentijd werd gegeven. Deze
treft u hieronder aan. GMST staat voor Greenwich Mean Sidereal Time.
GMST (0h) = 24110,54841s + 86 401 847,928 601s t + 9,313 216s t2 - 0,000 288s t3
-
0,019 514s
t4 +
0,000 123s t5 + 0,000 017s
t6
De
formule heeft als epoch J2000 en de waarde van “t” is het aantal
duizenden Juliaanse jaren vanaf J2000. “t” kunt u berekenen door T te
delen door 10.
Let
op! De uiteindelijke uitkomst van deze formule is de ST voor nul uur ‘s
nachts. Hierbij moet u dan nog de UT (GMT) bij optellen en klaar bent u.
In de formule zit de acceleratie van de ST er al in.
De formule is zo precies dat deze wordt
gegeven in seconden sterrentijd. Omzetting naar graden leidt
onherroepelijk tot verlies aan nauwkeurigheid.
Het rekenen met deze formule kan met de
meeste rekenapparaten al niet meer gebeuren, omdat deze het aantal cijfers
in het display niet kunnen herbergen. Computerprogramma’s werken met
variabelen, die in de uitgebreide precisie 18 cijfers achter de komma
kunnen onthouden, dus deze formule kan zonder problemen worden gebruikt in
een programma. Wij zullen een tweetal voorbeelden
uitwerken, zodat u de uitkomsten kunt controleren.
Eerste
voorbeeld
Het eerste voorbeeld is het
makkelijkst. Wij berekenen de Mean Sidereal Time op 1 jan. 2000 om 12h
UT (GMT). Dit is het begin van de nieuwe Epoch, zoals uitgebreid in deel-1
van deze serie is uitgelegd.
Hiervoor geldt:
JD = 2451545,0
T
= (2451545,0 - 2451545) / 36525 = 0
t
= T/10 = 0,0
In de formule hierboven zijn alle
termen met “t” erin gelijk aan nul, dus dat is makkelijk. Er blijft
dan alleen 24110,54841 sec. over voor de GMST
Wij delen dit door 3600 (3600 seconden
in 1 uur) en wij krijgen dan 6,697374558 uur en dit is meteen onze
uitkomst.
De uitkomst is gelijk aan 6h41m50,5484s.
Hierbij telt u de UT op, die was 12h precies.
De
einduitkomst is : 18h41m50,5484s.
Controle met een gewone nauwkeurige
efemeride gaat niet meer, die is gewoon te onnauwkeurig als u begrijpt wat
ik bedoel!
Ik controleer de
uitkomsten met een programma dat ik via het Jet Propulsion Laboratory (JPL)
in Massachusetts heb gekocht. Dit programma is een uiterst nauwkeurige
astronomische efemeride, die je zelf voor elke willekeurige tijd kunt
instellen tussen 1850 en 2050.
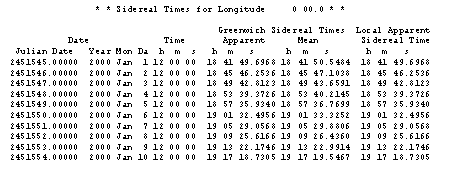
Een kleine listing uit dit programma is
in onderstaande figuur opgenomen, zodat u de door dit programma genoteerde
waarden van de Mean Sidereal Time kunt controleren.
Zoals u ziet, wijkt onze formule voor
de GMST niet af van de waarden die via het JPL komen.
In de tabel ziet u ook een kolom
Greenwich Apparent staan. Het is juist deze waarde die wij nodig hebben in
ons astrologisch programma, want hierin is de nutatie verwerkt. Zoals
eerder al vermeld, is de nutatie de ‘duw en trek’ aan de Aardas door
Zon, Maan en planeten.
|
|
De formule voor de Apparent Sidereal Time vindt u eerder in dit artikel.
Om de nutatie uit te rekenen, heeft u
eerst weer DR nodig. In deel-3 van deze serie is de waarde ervan al
berekend. Deze is 125o02’40,39816”=125,044555o
sin(DR)
= 0,8187
2
DR = 250,0891)
sin(2
DR) = -0,9402
NUT (lengte) = -17,23” x 0,8187 +
0,21” x -0,9402 = -14,30”(negatief).
De ecliptica op J2000 bedraagt 23o26’21,448”=
23,43929111
cos(ec) = 0,91748.
STAPP = GMST + NUTx cos(ec)/15
=
18h41m50,5484s.
+ (-14,30”) x 0,91748/15 = 18h41m50,5484s.
- 0,8747s = 18h41m49,6737s.
Vergelijkt u dit resultaat eens met de
tabel, die 18h41m49,6968s aangeeft.
Het verschil bedraagt 0,02
seconden, voorwaar geen slecht resultaat!
Ook hier hebben wij de sterk
vereenvoudigde formule voor de nutatie gebruikt. Toevallig ligt deze in de
buurt van de werkelijke waarde, die -13,968” bedraagt.
Als
u met de werkelijke waarde had gewerkt, dan kreeg u
STAPP = GMST + NUTx cos(ec)/15 =
18h41m50,5484s. + (-13,968”) x 0,91748/15 = 18h41m50,5484s. - 0,8544s = 18h41m49,6940s
met
slechts 0,002 seconden sterrentijd afwijking.
Hierbij
ziet u alweer hoe belangrijk het is om een goede formule te hebben voor de
nutatie. De nutatieproblematiek is niet gering, het benadert de
problematiek van de planetenberekening. In de volgende aflevering ga ik
uitgebreid in op de nutatieberekening.
De
nutatie gooit hier dus eigenlijk roet in het eten, want de formule voor de
GMST is zeer precies en zal veelal maximaal 0,001 seconde afwijken, maar
meestal ook minder.
Tweede
voorbeeld
Wij
zullen nu het tweede voorbeeld uitwerken en gebruiken weer dezelfde
gegevens : 13 november 1978 0h UT.
JD = 2443825,5
T = (2443825,5 - 2451545) / 36525 = -0,211 348 391 51
t = -0,021 134 839 151
t2 = 0,000 446 681 425
t3 = -0,000 009 440 540
t4 = 0,000 000 199 524
t5
= -0,000 000 004 217
t6
= 0,000 000 000 089
U ziet dat de waarden van t en hogere
machten van “t” in 12 decimalen zijn gegeven. Hierbij moet ik
eerlijkshalve zeggen dat de uitkomsten van de termen t3 t/m t6
nauwelijks meer bijdragen aan het resultaat, zoals u zelf later kunt zien.
GMST volgens de formule luidt :
24110,
548 41 +
-1 826 089,158 3
(t-term)
+
0,004 160 04
(t2-term)
+
0,000 000 002 72
(t3-term)
- 0,000 000 003 89
(t4-term)
- 0,000 000 000 000 51
(t5-term)
+
0,000 000 000 000 001
(t6-term)
Totaal : -1 801 978,6058 seconden
Delen door 3600 = -500,54961271 uur
Delen door 24 = -20,856233863 dagen
Is gelijk aan -0,856233863 dagen
Is gelijk aan
0,14376613688 dagen
Maal 24 = 3,450387285 uur
Is gelijk aan : 3h27m01,3942s
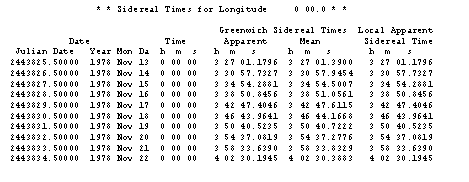
De GMST op 13-11-1978 kunt u
vergelijken met de waarde in onderstaande tabel.
Onze uitkomst
verschilt in dit geval 0,0042 seconden met de tabel en wij zullen
hiermee verder rekenen.
|
|
Om de sterrentijd voor de horoskoop te
krijgen, moeten wij de STAPP berekenen met behulp van de
nutatie en de ecliptica. Deze gegevens hebben wij al berekend in de
voorbeelden van de oude sterrentijdformule, helemaal aan het begin.
Het volstaat dan ook om hier alleen de
resultaten te geven.
De door mij gegeven vereenvoudigde
formule voor de nutatie leverde -1,90” op als nutatie.
Hierdoor wordt STAPP gelijk
aan :
3h27m01,3942s
+ (-1,90”)x0,91746/15 = 3h27m01,3942s -
0,12s = 3h27m01,2742s.
De tabel (JPL)
geeft 3h27m01,1796s.
Het verschil tussen onze berekeningen
en de tabel van het JPL bedraagt 0,0946 seconden en dit is eigenlijk te
veel.
Gebruiken wij echter de
vrijwel exacte waarde -3,373” als nutatie, dan wordt de STAPP:
3h27m01,3942s
+ (-3,373”)x0,91746/15 = 3h27m01,3942s
- 0,2063s = 3h27m01,1879s.
Wanneer wij deze waarde vergelijken met
de tabel van het JPL, dan is het verschil
teruggelopen tot 0,0083 seconden en hiermee zullen wij ons tevreden
moeten stellen.
Conclusies
Welke conclusies kunnen wij trekken uit
bovenstaande theorieën?
Allereerst moeten wij constateren dat
de eerst gegeven formule voor de ST een redelijk goed resultaat geeft.
Worden er geen extreem hoge eisen aan een computerprogramma gesteld, dan
kan met een gerust hart de formule worden gebruikt. Ik heb de formule
tenslotte zo’n 15 jaar lang gebruikt en de horoskopen waren altijd
redelijk exact.
De nieuwe formule is een sterke
verbetering. Wanneer wij de drie rekendatums gebruiken, nl. J1900, 13 nov.
1978 en J2000 en wij de resultaten met de oude- en nieuwe formule naast
elkaar zetten en deze vergelijken met de tabellen van het JPL, dan kunnen
wij onze conclusies trekken.
|
OUD |
JPL |
Formule. |
Verschil
in sec. |
|
J1900 |
45,8287 |
45,8360 |
0,0073 |
|
13-11-1978 |
01,3900 |
01,3200 |
-0,07 |
|
J2000 |
50,5484 |
50,4643 |
-0,0841 |
|
|
|||
|
NIEUW |
JPL |
Form. |
Versch. |
|
J1900 |
45,8287 |
45,8487 |
0,02 |
|
13-11-1978 |
01,3900 |
01,3942 |
0,0042 |
|
J2000 |
50,5484 |
50,5484 |
0 |
Gebruik van de nieuwe formule leidt vrijwel overal tot kleinere verschillen, dus een grotere nauwkeurigheid. Dit wordt beter, naarmate de datums dichter bij de nieuwe epoch J2000 liggen.
Globaal kan
gesteld worden dat bij datums tussen 1950 en 2050, dus symmetrisch rond
J2000, de verschillen tussen nul en 0,004
seconde zullen liggen.
Dit is een zeer aannemelijk
resultaat en geen enkele astrologische efemeride zal dit ooit publiceren.
Dit
betekent voor de berekening van de huizencupen een maximale fout in lengte
van ca. 0,02 boogseconde bij
normale snelheden van 1 graad per 4 minuten geboortetijd.
Bij een snelrijzende Ascendant (Vissen
op onze breedtegraden) zal hiermee de maximale fout in lengte ca. 0,16 boogseconde zijn.
Een dergelijk resultaat zal in de
eerstkomende 20 jaar niet worden geëvenaard.
Hierbij moet ik aantekenen dat we
tevens de nutatie onder ‘bedwang’ moeten zien te krijgen, omdat
hiervan de sterrentijd voor de horoskoop van belang is.
Dit onderwerp zal in de volgende
aflevering uitgebreid worden besproken.
-----
----- -----
Literatuur:
I.
Explanatory Supplement to
the Astronomical Ephemeris and the American Ephemeris - Nautical Almanac
Office, 1977
blz. 75;
II.
Bretagnon, P., et.al., “Theory of the rotation of the rigid Earth”,
1997, Astron.Astroph., 305-317;
______________________________________________
Pagina voor het laatst bewerkt op / Page maintained on: 31/12/2015