Astrologische Artikelen door J. Ligteneigen               

Home

Contact mail

Home > Artikelen > Artikel-3

Een klein vervolg op Artikel-2.

In deel-2 zijn we geëindigd met de meest recente formule voor de ecliptica, gebaseerd op de Epoch J2000 (1 jan. 2000 om 12.00 ET). De formule dateert van 1977 en geeft de hellingshoek van de ecliptica aan met een nauwkeurigheid van ca. 0,002". We hebben de invloed van de ecliptica gezien op de huizenposities en op de declinaties van de huizen.

U zult zich nu misschien afvragen: waarom deze ongehoorde precisie van 0,002"?

De formule is er nu eenmaal. Wanneer u hem toepast, rekent u meteen met de gegeven precisie. En als u de uitkomst bewaart (opschrijven, calculator, variabele in het programma), dan heeft u meteen de exacte waarde. Ook al denkt u nu geen gebruik te maken van deze precisie, hij is er gewoon... dus gebruik het.

Ook bij de berekeningen van de declinaties van de planeten wordt de ecliptica gebruikt en ook bij de voorbereidende berekeningen van de planeetlengten. Als u bijvoorbeeld de planeten met 0,5 boogseconde wilt berekenen, dan moeten in het voorbereidende traject alle bestanddelen nauwkeuriger zijn dan het eindresultaat, anders zou door opeenstapeling van afrondingen het gewenste eindresultaat niet meer haalbaar zijn.

0,5 boogseconde voor planeten? Kan dit? Jawel, het kan. De gigantische vooruitgang in observaties maken het mogelijk Zon, Maan en planeten waar te nemen met 0,05 boogseconden, soms zelfs beter. Dit heeft geleid tot een soort wedloop tussen de observaties en de wiskundige berekeningen. Genoeg stof voor de komende afleveringen.

We zullen ons nu gaan richten op de berekening van de Maansknoop ofwel de Draconis.

===========================     Mean Lunar Node (MLN)     ===========================

Soms is het onvermijdelijk om Engelse termen te gebruiken. Hoewel ik zelf voorstander ben van zoveel mogelijk Nederlands taalgebruik (er wordt al zoveel ver-engelst), komen we in efemeriden (de meeste zijn Engelstalig) ook deze benamingen tegen.

Mean Lunar Node is het best te omschrijven als de  Gemiddelde Maansknoop.

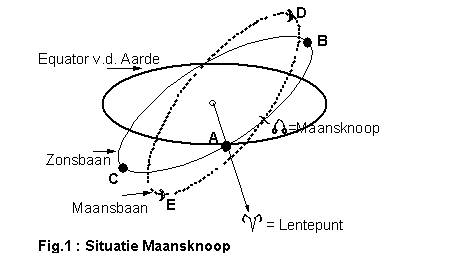
Wat dit begrip voorstelt, heb ik in Fig. 1 getekend. De liggende ellips stelt de equator van de Aarde voor. 

De Zonsbaan is aangegeven door de schuine met doorgetrokken lijn getekende ellips. Deze zonsbaan is de ecliptica, waarop deel-2 uitvoerig is ingegaan. Bij punt "A" kruist de zonsbaan de Aardequator en dit punt heet het lentepunt, ofwel equinox en is altijd het punt 0 graden Ram, derhalve ingetekend met het Ram-symbool. Vanaf dit punt begint de telling van de lengten van de hemellichamen.

Bij punt "B" heeft de Zon 90 graden afgelegd, sinds het lentepunt en hij bereikt hier zijn grootste noordelijke declinatie op 0 graden Kreeft. Daarna vervolgt de Zon zijn weg langs de ecliptica en komt uit bij punt "C" op 0 graden Steenbok, waar hij zijn meest zuidelijke declinatie bereikt. Daarna komt de Zon weer bij punt "A" en begint alles opnieuw.

De Maan loopt ook in een ellipsvormige baan en die is aangegeven door de schuine ellips met stippellijn. De maansbaan kruist de zonsbaan in het punt, aangegeven met het Draconis-symbool. Bij punt "D" bereikt de Maan haar meest noordelijke declinatie, daarna doorloopt zij haar baan en komt in punt "E", waar zij haar meest zuidelijke declinatie bereikt.

De Draconis, ook wel de Noordelijke Maansknoop genoemd, heet zo, omdat de declinatie van de Maan na het passeren ervan Noordelijk wordt. Dit kunt u ook in de tekening zien: De Maan staat 'boven' de zonsbaan. Precies aan de overkant bevindt zich de Zuidelijke Maansknoop. Na het passeren ervan krijgt de Maan een zuidelijke declinatie.

De Noordelijke Maansknoop wordt ook wel drakenkop genoemd en de Zuidelijke variant heet drakenstaart. 

In de meeste computerprogramma's wordt de volgende formule gebruikt, die afkomstig is van E.W. Brown¹ :

De Epoch in deze formule is J1900.

Hoe u T moet berekenen is in deel-1 uitgelegd.

Let u goed op het minnetje en de plusjes.

Ik heb zelf deze formule jarenlang gebruikt.

Wij zullen de lengte van de Draconis berekenen op twee momenten, nl. J1900 en J2000. Aangezien deze formule als Epoch J1900 heeft, is T gelijk aan nul voor J1900 en gelijk aan 1 voor J2000.

J1900 = 31 dec. 1899, 12^h UT:

MLN = 259⁰10' 59,79"  (J1900)

J2000 = 1 jan. 2000, 12^h ET:

MLN = 259⁰10' 59,79" - 1934⁰08' 31,23" + 7,48" + 0,008" = -1674⁰57' 23,952"

Negatieve graden omzetten in positief geeft: 125⁰02' 36,049" (J2000).

Deze standen zijn exact. Het kan zijn dat uw rekenmachine afrondt als u de getallen gaat invoeren. Dit gebeurt nl. bij het getal -1934⁰08'31,23". Het aantal cijfers is vaak teveel voor het display. U kunt dit ondervangen door als volgt in te voeren : -1934 -8/60 - 31,23/3600. Het rekenapparaat rekent dan correct. Als u programmeert en u declareert een variabele als REAL(Pascal) of als DOUBLE PRECISION(Basic) dan heeft u hier geen last van. U moet wel eerst zelf de graden, minuten, seconden omzetten naar een decimaal getal.

Zoals ik al schreef is de tijd niet stil blijven staan, sinds Brown's tabellen uit 1919. Recentelijk (sinds 1982) heeft het Franse echtpaar Chapront² een volledige Maantheorie uitgewerkt met een gigantische nauwkeurigheid. Onderdeel daarvan is natuurlijk de Mean Lunar Node, die door hen wordt gegeven door de volgende nieuwe formule, gebaseerd op Epoch J2000:

Als u op basis van de Epoch-1900 formule de Draconis heeft berekend voor J2000, dan ziet u dat de uitkomst van 125⁰02' 36,049" en klein verschil maakt met de recentere en juiste waarde van 125⁰02' 40,39816".

Het verschil is 4,36" per 100 jaar, lopende vanaf J1900 tot J2000.

We doen nu hetzelfde met de nieuwe formule. We rekenen de Draconis uit voor J1900 en J2000, uiteraard nu op basis van de Epoch J2000.

Voor J1900 geldt nu: T=-1 en voor J2000 geldt nu: T=0.

J1900:

MLN = 259⁰10' 58,1499"

J2000:

MLN = 125⁰02' 40,39816"

Het verschil bij J2000 is uiteraard nul en bij J1900 is het verschil gelijk aan:

58,1499" - 59,79" (de waarde volgens Brown) = 1,64". Hier bedraagt het verschil dus 1,64" per 100 jaar, dus aanmerkelijk kleiner!

In Fig. 2 laat ik u zien wat er gebeurt met de Maansbaan in de loop der tijd.

Het snijpunt van de Maans- en Zonsbaan is de Draconis Nr.1.

Enige jaren later is de Maansbaan een beetje teruggedraaid, zodat Maansbaan nr. 2 ontstaan is. Het nieuwe snijpunt is nu de Draconis Nr.2.

Dit langzaam terugdraaien van de Maansbaan wordt in de nieuwe formule aangegeven met -1934⁰08'10,26"T. In 1 Juliaanse Eeuw (36525 dagen) draait de Maansbaan dus ruim 5 rondjes in teruggaande beweging. Een ronde wordt afgelegd in ca. 18,6 jaar.

Soms valt de Maansknoop precies op de lente-equinox. In die tijd kan de Maan een maximale declinatie van ruim 28⁰ N bereiken. 9,3 jaar later (een halve omloop) valt de Draconis samen met de herfst-equinox en dan haalt de Maan  slechts 19⁰ N. declinatie. Weer 9,3 jaar later is het weer andersom.

Precisie van de nieuwe formule

Met de nieuwe formule wordt in 100 jaar rondom J2000 (dus van 1900 tot 2100) een afwijking van ca. 1,64" bereikt. Bij de meeste toekomstige horoskopen (tussen 1950 en 2050) zal de maximale afwijking ca. 0,5" zijn, dus mogen wij ons tevreden stellen met deze resultaten.

Nutatie

Ook in de vorige aflevering schreef ik al dat de nutatie verwerkt moet worden in de lengte van de hemellichamen en in de helling van de ecliptica.

Met andere woorden, de door ons berekende Draconis is nog niet helemaal te vergelijken met de stand in de efemeride.

In de efemeriden wordt de nutatie meegenomen in de standen, hetgeen uiteraard correct is.

De theorie van de nutatie is dermate complex dat dit hier nog niet gepast is om het te behandelen. In deel-5 van deze serie zal ik hieraan uitgebreid aandacht besteden.

Om een héél klein voorschotje te nemen op de nutatie geef ik hier alvast de twee belangrijkste wiskundige termen, die uitsluitend afhankelijk zijn van de lengtegraad van de draconis. Hiermee kunt u de uiteindelijke draconis met 0,5 tot 1,0 boogseconde nauwkeurig berekenen. De zeer sterk vereenvoudigde formule voor de nutatie luidt:

Hierbij teken ik aan dat de twee termen afgerond zijn, omdat het hier geen zin heeft om nauwkeurigheid te pretenderen en toch maar twee termen te hanteren.Alle overige termen van de nutatie in lengte zijn combinaties van andere factoren, die dus in aflevering-5 aan de orde komen.

Enkele rekenvoorbeelden:

De Draconis op J1900 = 31 dec. 1899 12^h UT.

Volgens de meest recente formule :

Œ =259⁰10'58,1499" = 259,1828192⁰

sin(Œ) = sin(259,1828192) = -0,982231;

sin(2x Œ) = sin(518,3656) = 0,368682;

Nutatie (lengte) = -17,23"x -0,982231 + 0,21"x 0,368682 = 17,00"

Deze nutatie telt u op bij de reeds berekende Draconis, zodat u krijgt:

Œ =259⁰ 11' 15,2". De zodiakpositie is : 19⁰ 11' 15" Boogschutter.

Volgens de Concise Planetary Ephemeris staat de Draconis op 19⁰11'18" Boogschutter, maar in deze efemeride zijn de posities afgerond op 6".Onze formule is vele malen nauwkeuriger dan de efemeride.

Overigens is de nutatie in lengte volgens een zeer nauwkeurige berekening gelijk aan : 17,377", dus onze eenvoudige benadering zat er niet veel naast.

Voorbeeld op J2000 = 1 jan. 2000 om 12^h ET.

De reeds berekende Draconis was :

125⁰ 02' 40,398" = 125,044555⁰.

sin(Œ) = sin(125,04455) = 0,8187;

sin(2 Œ) = sin(250,0891) = -0,9402;

Nutatie in lengte = -17,23" x 0,8187 + 0,21" x -0,9402 = -14,30". De nutatie is hier dus negatief (het minteken).

We tellen (de negatieve) nutatie op bij de eerder berekende Πen krijgen :

Œ = 125⁰ 02' 26". De zodiakpositie is gelijk aan 5⁰ 02' 26" Leeuw.

De Complete Planetary Ephemeris geeft een stand aan van 5⁰ 02' 18" Leeuw. Deze efemeride werd gemaakt in 1975 en rekende nog met de oude formule van de Draconis, die zoals u kunt controleren, 4,36" lager uitkomt. Als deze efemeride met de nieuwe formule had gewerkt, dan was de uitkomst waarschijnlijk 5⁰02'22" Leeuw geweest. Ook deze efemeride rondt af op 6".

De nutatie, volgens de zeer nauwkeurige formules zou -13,968" moeten zijn. Ook hier is onze sterk vereenvoudigde formule er niet ver naast met -14,30".

U kunt de formules rustig uitproberen met willekeurige datums en uw eigen geboortetijd. De formule voor de Draconis is ook voor grotere periodes geldig en nauwkeurig. U moet hierbij denken aan het tijdinterval 4000 v.Chr. tot 8000 AD. Dit is hetzelfde tijdinterval, waarmee de Maantheorie volgens Chapront is opgebouwd.

Kleine waarschuwing

De hier gegeven nutatie-formule geldt alleen voor de lengte van hemellichamen en dus NIET voor de hellingshoek van de ecliptica. Deze formule zal in aflevering-5 in nauwkeurige vorm worden gegeven.

Lunar Node en de efemeriden

Voor de 21e eeuw zijn door Neil F. Michelsen twee soorten efemeriden uitgegeven, nl. de compacte vorm van The American Ephemeris, die loopt van 2000 tot 2050 en de uitgebreide versie van The American Ephemeris, die alleen in delen van 10 jaar wordt uitgegeven. In Sagittarius ziet u altijd een kopie uit de compacte versie. Het zal u hierin zijn opgevallen dat de Mean Node niet meer per dag wordt gegeven, maar slechts 1 keer per maand en wel op de eerste van de nieuwe maand, onderaan bij Astro Data. Dit is erg vervelend, want u moet dan nog even flink rekenen om op juiste wijze te intepoleren. In de uitgebreide versie vindt u de Mean Node wel elke dag genoteerd. Bovendien heeft u bij deze uitgebreide versie ook de declinaties die bij de compacte efemeride ook ontbreken. In Sagittarius 1984, nr.1 heeft Theo v. Berkel³ een goed artikel hierover geschreven, zodat ik u hier naar kan verwijzen.

True Node

Zowel in de compacte als in de uitgebreide versie van The American Ephemeris komt u de kolom "True Node" tegen.

Deze kan zelfs retrograde lopen! Wat is nu die True Node en hebben we die nodig?

Het betreft niet een nieuw ontdekte Maansknoop of zoiets. Het is een formulering uit de astronomie, die de toestand van de Maanpositie uitdrukt in zogenaamde "osculating elements". Dit zijn baanelementen van de Maan, die haar toestand in de ruimte volledig beschrijven, inclusief de verstoringen in de baan.

Ik heb zelf geen praktische ervaring met de True Node, omdat ik altijd de Mean Node gebruik, die eigenlijk altijd voldaan heeft. Juist zijn tergend teruglopende beweging van 3'12" per jaar progressief zorgt ervoor dat ingaande aspekten een lange voor- en nawerking hebben, maar ook zeer intensief werken! In Sagittarius komt u hierover veel voorbeelden tegen. Leest u bijvoorbeeld eens Sagittarius 1998, Nr.1 over de karakteristieke en concrete uitwerking van Draconis⁴.

Het zou interessant zijn als er mensen zijn die hiermee concreet gewerkt hebben en die er goede resultaten mee boeken. Je zou je kunnen voorstellen dat aspekten op een retrograde True Maansknoop anders uitwerken dan aspekten op de een rechtlopende True Maansknoop. Opeens dienen zich dan veel varianten aan, zoals aspekten met en van de Mean Draconis en aspekten met en van de True Maansknoop. Eerlijk gezegd weerhoudt iets mij ervan dit te gaan toepassen, ik weet niet waarom. Misschien is het toch de betrouwbaarheid van de reeds opgedane ervaringen met de Mean Draconis. Het is altijd moeilijk om van het bekende pad af te wijken en je in iets onbekends te storten. Hiertegenover staat dat het geen kwaad kan om iets te onderzoeken met behoud van het goede! Als de voorvechters van de planeet Pluto (zoals onze hoofdredacteur) zich geen moeite hadden getroost om Pluto te onderzoeken en toe te passen, dan waren we nog even ver als in 1930!

Formules voor de True Node vindt je niet zo vaak en als je ze vindt, dan zijn ze vrij onnauwkeurig. In een boek van Michael Erlewine⁵ uit de beginjaren '70 wordt een formule gegeven, die slechts 5 wiskundige termen bevat, die ik u hieronder zal geven. Elke term bestaat uit zogenaamde 'argumenten', die vooraf berekend moeten worden, op dezelfde wijze zoals de Draconis werd berekend. Erlewine's formule luidt als volgt:

True Node = Mean Node (inclusief nutatie) - 5392"x sin(2D-2F) - 541" x sin(L') - 442" x sin(2D) + 423" x sin(2F) - 291" x sin(2L-2F).

Deze formule levert een precisie van ca. 20 boogminuten op, dus niet erg zuiver.

De formules van de argumenten zijn (Epoch J1900):

D = 350,737⁰ + 445 267,11⁰ T;

F = 11,251⁰ + 483 202,02⁰ T;

L = 296,104⁰ + 477 198,85⁰ T;

L' = 358,475⁰ + 35 999,05⁰ T.

Grotere precisie voor de argumenten is niet nodig, omdat het slechts hulpfactoren zijn in verdere berekeningen.

We zullen een voorbeeld geheel uitwerken, waarvan u de uitkomst kunt controleren in Sagittarius, Nr. 3 van dit jaar.

Gevraagd: de Mean Πen de True Πvoor 1 juni 1999 om 0^h UT, zoals ook de compacte efemeride rekent.

In diezelfde efemeride ziet u dat Delta-T  in 1999 al 61 seconden bedraagt. Deze Delta-T moet u optellen bij de UT(de oude GMT) en daarmee krijgt u de ET, waarop alle gegeven formules betrekking hebben.

0^h UT is dus 0.01.01 ET. Als fractie van de dag is dit 61 / 86400 = 0,000706.

M=6, dus m=6, y=1999.

B=INT(1999/400) - INT(1999/100) = -15 en C=0 (want y is groter dan nul).

JD = 2451330,500706

Voor Epoch-J1900-formules:

T = (JD - 2415020) / 36525 = 0,994127328

Voor Epoch-J2000-formules:

T = (JD-2451545) / 36525 = - 0,005872671

Met deze T rekenen we de Mean Draconis uit (epoch-J2000-formule).

Œ = 136⁰24' 11,16" = 16⁰24' 11" Leeuw.

Hieraan moet nog de nutatie worden toegevoegd, dus rekenen we uit:

sin(Œ) = 0,68958

sin(2x Œ) = -0,99880

NUT = -17,23" x 0,68959 + 0,21" x -0,99880 = -12,09"

Mean Node = 136⁰24'11" - 12,09" =

136⁰23'59" = 16⁰23' 59" Leeuw.

In de efemeride leest u de stand af onder Astro Data = 16⁰23' 54" Leeuw. De efemeride rondt af op 6" nauwkeurig.

Berekening True Node. 

Hiervoor moeten wij eerst de 'argumenten' D, F, L en L' berekenen volgens de gegeven formules.

D = 350,737⁰ + 445267,11⁰ x T

D = 202,9392⁰

F = 11,251⁰ + 483202,02⁰ x T

F = 135,5839⁰

L = 296,104⁰ + 477198,85⁰ x T

L = 212,5217⁰

L' = 358,475⁰ + 35999,05⁰ x T

L' = 146,1144⁰

2D-2F = 134,7106⁰

sin(2D-2F) = 0,710669

L' = 146,1144⁰

sin(L') = 0,557536

2D = 405,8784⁰ = 45,8784⁰

sin(2D) = 0,717864

2F = 271,1678⁰

sin(2F) = -0,999792

2L-2F = 153,8756⁰

sin(2L-2F) = 0,440322

True Node = Mean Node (136.23.59)

      - 5392" x 0,710669             = -3831,9"

      -541" x 0,557536                = -301,6"

      - 442" x 0,717864               = -317,3"

      + 423" x -0,999792             = -422,9"

      - 291" x 0,440322               = -128,1"

Het totaal van alle 5 factoren tezamen is gelijk aan -5001,8" = -1⁰23' 21,8"

True Node is derhalve : 136⁰23' 59" -

1⁰23' 22" = 135⁰00' 37" = 15⁰00' 37" Leeuw.

De efemeride geeft 14⁰55' 30" Leeuw afgerond op 6" nauwkeurig.

U ziet het al, onze eigen formules voor de True Draconis zijn nog niet volledig. Het betrof ook slechts de 5 termen uit het boek van Erlewine.

Het echtpaar Chapront heeft in hun zeer nauwkeurige Maantheorie ook formules gegeven voor de "osculating elements". Zelfs met hun  641 storingstermen in lengte, 328 termen in breedte en 355 termen in afstand is het niet mogelijk om de True Node nauwkeuriger te geven dan ca. 9", alhoewel zij met die formules de lengte van Maan op ca. 0,5" precies kunnen geven. Dit geeft enig beeld hoe extreem moeilijk de berekening van de True Node in elkaar zit. Slechts met de meest uitgebreide Maantheorie van de Chapront's met ruim 20.000 termen in lengte, 7500 termen in breedte en 9600 termen in afstand kan de True Node binnen de 0,1" onder 'bedwang' worden gehouden.

Als simplistische oplossing hebben de Chapront's de 22 grootste termen gepubliceerd, waarmee op eenvoudige wijze de True Node kan worden berekend. Deze wijze is volledig analoog aan onze 5 belangrijkste termen in dit artikel. Op verzoek kunnen deze 22 termen beschikbaar worden gesteld, waarmee de True Node op ca. 72" nauwkeurig kan worden berekend.

De volgende keer wordt de berekening van de Sterretijd behandeld met een te behalen precisie van 0,002 sec.

Literatuur:

i.       E.W. Brown, "Tables of the Motion of the Moon", New Haven, 1919;

ii.      M. Chapront-Touzé, J. Chapront, Astron. Astroph., 190, (1988);

iii.     Th. v. Berkel, Sagittarius, 1, (1984);

iv.     J.B. Gieles, Sagittarius, 1, (1998);

v.      M. Erlewine, Manual Of Computer Programming For Astrologers;

______________________________________________

Pagina voor het laatst bewerkt op / Page maintained on:   31/12/2015