Astrologische Artikelen door J. Ligteneigen
Oplossing vraag uit Artikel-1.
We zijn deel-1 min of meer geŽindigd
met het feit dat er in de IAU (1976) System of Astronomical Constants een
nieuwe Epoch is gedefinieerd met de aanduiding J2000.0 en die begint op 1
januari 2000 om 12h ET.
De formule voor de berekening van JD,
zoals die in de vorige aflevering is gegeven, was gebaseerd op UT. Maar de
formule geldt evenzeer voor tijden in ET. U vervangt UT in de formule door
ET en u krijgt een juist resultaat.
Y=2000;
M=1; D=1; ET=12.00.00
M=1, dus volgens stap(2):
m
= M+12 = 13; y = Y-1 = 1999
ET / 24 = 0,50.
De datum is groter dan 15.10.1582, dus:
B=INT(y/400) -
INT(y/100)= 4 - 19=-15
Het jaartal y is groter dan nul, dus
C=0.
INT(365,25*y
- C) = 730134
INT(30,6001*{m+1}) = 428
JD
is nu
: 730134 + 428 - 15 + 1720996,5 + 1 + 0,5 = 2451545,0
De Juliaanse Eeuw wordt berekend
middels : T = (JD-2415020)/36525
T
is dus
: (2451545,0 - 2415020)/36525 = 1,0
Berekend
t.o.v. de Epoch J1900.0 heeft
T dus de waarde 1,0.
Aangezien J2000.0 als nieuwe epoch is
aangewezen, moet ook de formule van de Juliaanse Eeuw gebaseerd worden op
de nieuwe epoch. De formule van T wordt dan :
|
T
= (JD - 2451545) / 36525 (Epoch
J2000.0) |
Als u nu T opnieuw uitrekent, dan krijgt u de waarde 0,0.
Het is dus wel goed opletten op welke
epoch T is gebaseerd. Bij elke nieuwe formule, waarin "T"
voorkomt, zal ik dan ook aangeven op basis van welke epoch die gebaseerd
is.
ET
of UT gebruiken in formules?
Het is voor de bepaling van de Zon,
Maan en planeten, de Ecliptica en de Draconis standaard om ET te
gebruiken.
ET staat voor Efemeriden Tijd (Ephemeris
Time) en is de ideale onafhankelijke tijdsmaat voor de berekening van de
posities van de hemellichamen.
Zoals u wellicht weet, verschilt ET van
de UT (de oude benaming was GMT, maar dit wordt eigenlijk niet meer
gebezigd). Doordat de draaiing van de Aarde om zijn eigen as een
voortdurende en onvoorspelbare vertraging oploopt (door getijdenbewegingen
van zeeŽn en oceanen, vulkaanuitbarstingen en allerlei andere optredende
gebeurtenissen), is UT geen goede tijdsmaat.
Alleen voor de theoretische berekening
van de Sterretijd (Sidereal Time) dient uitgegaan te worden van de UT. Dit
is ook in de astronomie gebruikelijk.
In een apart artikel over TIJD en
tijdsrekening zal ik u hier alles over duidelijk maken.
Als u nu al meer wilt weten over het
verschil tussen ET en UT/GMT, dan dient u Sagittarius 1983-nr.4 te
raadplegen. Theo van Berkel heeft een erg goed stuk geschreven over de
toepassing van ET en GMT bij het gebruik van een efemeride.
In Sagittarius 1985-nr.5 vindt u ook
nog aanvullende informatie.
============================
De ecliptica.
==================================
De Aarde draait om zijn as in bijna 24
uur. Echter deze as staat niet 'recht', maar staat schuin ten opzichte van
de baan, die de Aarde bezet in zijn beweging om de Zon. Doordat deze hoek
bestaat, is er sprake van seizoenen, zoals schematisch in Fig. 1 is
aangegeven. Was deze hoek er niet, dan waren er ook geen seizoenen
mogelijk.
In Fig. 1 is de baan van de Aarde om de
Zon heen sterk overdreven elliptisch getekend. In werkelijkheid is de baan
vrijwel cirkelvormig, maar formeel is het een ellips. Alle planeten, die
om de Zon draaien, doen dit in een ellipsvormige baan. De baan van
Mercurius bijv. is wel sterk elliptisch en komt nog het meest overeen met
Fig. 1.
Merk op dat de schuine as altijd
dezelfde kant op wijst, waar de Aarde zich ook bevindt in zijn baan om de
Zon.
Het interessante is dat in de
zomerperiode de Aarde eigenlijk het verst verwijderd is van de Zon.
Doordat de schuine as in de zomer naar de Zon toe gericht is, bereiken de
zonnestralen voornamelijk het noordelijk halfrond van de Aarde en daar is
het dan het warmst.
In de winter bevindt de Aarde zich ook
het verst weg van de Zon, maar doordat de schuine as van het zuidelijk
halfrond naar de Zon toe is gekeerd, bereiken de zonnestralen nu
voornamelijk het zuidelijk deel van de Aarde en het is juist daar zomer,
terwijl het bij 'ons' winter is.
In de lente en herfst bevindt de Aarde
zich het dichtst bij Zon. De aardas is nu niet naar de Zon toe gericht en
de zonnestralen bereiken zowel het noordelijk- als het zuidelijk halfrond
min of meer even veel.
Het verschil in afstand tussen
lente/herfst en zomer/winter tussen Aarde en Zon bedraagt al gauw zo'n
ruime 5 miljoen kilometer.
Hoe
wordt de schuine hoek bepaald?
U heeft zich wellicht al eens
afgevraagd hoe nu eigenlijk de eclipticahoek wordt gemeten. In atlassen en
informatieve boekjes staat veelal dat deze hoek ongeveer 23o26'
bedraagt.
Al voor het einde van het tweede
millennium voor Christus deden de BabyloniŽrs en de Egyptenaren al
metingen aan de Zon. Hiervoor maakten zij gebruik van een lange stok, de
zgn. gnomon.
Zo'n gnomon was bijv. 1 meter hoog.
Door nu op het langste dag van het jaar de schaduw te meten, die de gnomon
op de vlakke grond afbeeldt, kan de ecliptica gemeten worden.
Hiervoor moest men nog een gegeven
weten, nl. de breedte van de plaats van waarneming.
Zo mat de Griekse geleerde Erathostenes
(276 v.C - 195 v.C.) de ecliptica op twee plaatsen, nl. AlexandriŽ en
Syene (het moderne Aswan in het Zuiden van Egypte).
Precies op de dag van het
zomersolstitium stond de Zon pal in het Zenit. De ecliptica werd berekend
als: Breedte plaats van waarneming minus Zenitafstand van de Zon.
Voor Syene had Erathostenes de breedte
bepaald op 23o51'20" NB. Omdat de Zenitafstand nul was (de
Zon stond pal boven zijn hoofd), was de ecliptica ook gelijk aan 23o51'20".
Voor AlexandriŽ zei hij dat de
Zenitafstand 1/50-ste deel van een cirkel was (is gelijk aan 7o12').
Omdat Erathostenes dacht dat AlexandriŽ
precies ten Noorden van Syene lag, beredeneerde hij dat de afstand van
Syene tot AlexandriŽ gelijk was aan 1/50-ste deel van de omtrek van de
Aarde. De afstand Syene-AlexandriŽ was destijds op 5000 'stades' bepaald.
De omtrek van de Aarde moest dan 50 x 5000 = 25.000 'stades' zijn. De
lengte van een 'stade' is eigenlijk onbekend en ook de waarneming 1/50-ste
deel van een cirkel is waarschijnlijk afgerond. Niettemin
is het interessant om te weten dat de eerste waarnemingen van Erathostenes,
waarvan cijfermateriaal bekend is geworden, als een der eersten de omtrek
van de Aarde bepaalde.
Ook heeft Erathostenes een fout gemaakt
in zijn waarnemingen. Zo ligt Syene (ofwel Aswan) niet op 23o51'20",
maar op 24004'38" NB. AlexandriŽ ligt op 31o11'10"
NB waar Erathostenes uitging van 30o58' NB. Ondanks de fouten
waren de waarnemingen bijzonder nauwkeurig, zoals we later zullen
narekenen. De eclipticahoek volgens de formule (die later volgt) was in
die tijd : 23o43'35". Erathostenes zat er dus 'maar' een
kleine 8 boogminuten naast!
De meeste waarnemingen van de ecliptica
in de oudheid werden door de Chinezen gedaan, maar ook de Arabieren waren
meesters in de waarneming en wiskundige berekeningen.
In onderstaande tabel ziet u enige
waarnemingen uit deze oudheid.
Ook zijn een paar recentere
waarnemingen toegevoegd.
Het is van het allergrootste belang
geweest dat deze waarnemingen zijn vastgelegd. Mede hierdoor zijn de
lange-termijn-bewegingen van de ecliptica bepaald en dit voor grote waarde
voor een aantal toepassingen, zoals efemeriden, astro-archeologie,
paleoklimatisch onderzoek, etc.
|
epoch |
bron |
T |
ecliptica |
|
-1100 |
Chou Li |
-30.0 |
23.881 |
|
-350 |
Pytheas |
-22.5 |
23.819 |
|
-250 |
Erathostenes |
-21.5 |
23.856 |
|
-150 |
Hipparchos |
-20.5 |
23.858 |
|
-114 |
Greece |
-20.1397 |
23.7183 |
|
-30 |
Liu Hsiang |
-19.2997 |
23.745 |
|
89 |
Chia Khuei |
-18.1097 |
23.66 |
|
173 |
Liu Hung & T. Yung |
-17.2697 |
23.837 |
|
173 |
Liu Hung & T. Yung |
-17.2697 |
23.689 |
|
178 |
Liu Hung & T. Yung |
-17.2197 |
23.631 |
|
450 |
Tsu Chhung-Chih |
-14.4997 |
23.636 |
|
630 |
Li
Shun-FÍng |
-12.6997 |
23.661 |
|
1587 |
Tycho
Brahe |
-3.1297 |
23.5067 |
|
1690 |
Flamsteed |
-2.0999 |
23.4835 |
|
1800 |
Bessel |
-1.00000 |
23.465222 |
|
1850 |
Leverrier |
-0.50000 |
23.458842 |
|
1900 |
------ |
0.00000 |
23.452174 |
Door deze supernauwkeurige waarnemingen
is het mogelijk geworden dat de hellingshoek van de ecliptica tot op 0,001
boogseconde nauwkeurig berekend kan worden.
De
formule voor de Ecliptica
De formule voor de hellingshoek van de
ecliptica, die al ettelijke decennia in gebruik is, luidt als volgt :
|
E = 23.452294o
- 0.0130125o T
- 1.64o.10-6
T2
+ 5.03o.10-7 T3 Epoch is : J1900 |
Waar u "T" ziet staan,
vermenigvuldigt u het getal dat ervoor staat met T.
Waar T2 staat,
vermenigvuldigt u het getal dat ervoor staat met TxT (ofwel T-kwadraat).
Waar T3 staat, vermenigvuldigt u het getal dat ervoor staat met TxTxT
(ofwel T tot de derde macht).
1,64o.10-6
betekent 1,64 met 6 nullen ervoor, dus : 0,000 000 164.
Let u vervolgens goed op alle plusjes
en minnetjes.
Als we bijvoorbeeld de ecliptica
uitrekenen voor de Epoch zelf, dus 31 dec. 1899 om 12h UT,
waarvoor geldt dat T gelijk is aan nul, dan is de ecliptica dus 23.452294o
= 23o27'08,258".
In de tijd van Erathostenes (het jaar
-250 ongeveer), is T gelijk aan -21,5.
T2 is dan 462,25 en T3
is : -9938,375.
De
ecliptica
in zijn tijd was derhalve:
23,452294 + 0,279768 - 0,000758 -
0,004999 = 23,726305 = 23o43'35".
Controleert u dit nog even met de tekst
van de vorige bladzijde en merk op hoe nauwkeurig voor die tijd er te werk
is gegaan door de oude meesters.
In de gegeven formule voor de ecliptica
ziet u de wiskundige term -0,0130125o T staan. Die staat voor
de lineaire afname (het minteken) per Juliaanse Eeuw van de ecliptica. Met
andere woorden: de hellingshoek wordt ieder jaar kleiner en het tempo
ervan komt overeen met 46,845" per Juliaanse Eeuw. Dat is niet erg
veel, maar in de loop van honderden jaren wordt deze afname toch
betekenisvol. Met name voor onderzoekers op paleontologisch gebied is dit
van belang, want de verandering van het klimaat houdt verband met deze
hellingshoek. Zoals u in Fig. 1 kunt zien, is de hoeveelheid warmte die
het noordelijk- of zuidelijk halfrond ontvangt, afhankelijk van de
ashelling.
Het optreden van ijstijden, verdwijnen
of verschijnen van diersoorten is hieraan gerelateerd.
Geldigheid
van de formule
De formule voor de ecliptica dient
echter niet voor onbepaalde tijd toegepast te worden. Veilige grenzen zijn
T= - 100 tot +100, ofwel een tijdvak van ca. 10.000 jaar vůůr en nŠ
J1900.
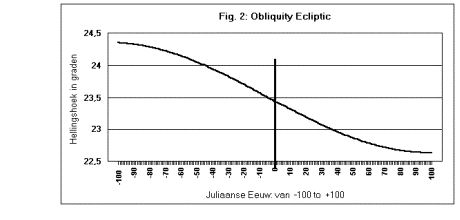
Hierbuiten komen er grote afwijkingen. Zo is bijv. bekend dat in het jaar 47.000 v.Chr. (T=-489) de ecliptica ca. 24,4o was. Gaat u de formule klakkeloos toepassen, dan komt u uit op min 29,34 en dat is onmogelijk, want de hellingshoek kan niet negatief worden.
|
|
U kunt uit de grafiek (de formule is in een spreadsheet ingevoerd) al een beetje zien dat de daling van de eclipticahoek niet permanent doorloopt. Hij vlakt af en de ecliptica wordt niet kleiner dan 22,5 graden. Ook het maximum zal niet hoger worden dan zo'n 24,5 graden.
Een
formule voor oudheidkundig onderzoek.
Uit het grote aantal waarnemingen uit
de oudheid en ook uit de gigantische hoeveelheid waarnemingen in deze
eeuw, is door Wittman4 een formule samengesteld, die:
(1)
de meest nauwkeurige waarnemingen na 1700 in zich herbergt;
(2)
nauwkeurig is voor waarden van T>= +100 en T<=-100;
(3)
het cyclisch patroon van ongeveer 410 eeuwen volgt.
Wittmann komt met de volgende formule,
gebaseerd op epoch J1900:
![]()
Hierbij hebben
![]() de
volgende waarden:
de
volgende waarden:
![]()
![]()
![]()
![]()
Ik zal u een rekenvoorbeeld geven.
Op de epoch J1900 is T gelijk aan nul.
T+
![]() 3,40.
3,40.
![]()
sinus (0,052088 radialen) = 0,05206445
0,86 maal 0,05206445 = 0,044775
23,496932 - 0,044775 = 23,452157
De ecliptica is derhalve 23o27'07,764"
Deze formule is ALLEEN voor historische
doeleinden te gebruiken. Voor onze precisieberekeningen hanteert u de
eerder gegeven formule.
Hieronder ziet u wat het effect is van de historische formule op de ecliptica voor een periode van T=-1000 tot T=+1000, ofwel een periode van 200.00 jaar!
|
|
De invloed van de ecliptica op de horoskoophuizen.
De eclipticawaarde heeft invloed op de
berekening van alle huizen van de horoskoop. Wij zullen de cusp van het MC
gaan uitrekenen voor een Sterretijd van 3 uur precies voor een ecliptica
van jet jaar 1950 en 2000 resp.
Aan de hand van de precisieformule voor
de ecliptica berekenen wij de beide ecliptica's.
EC(1950)
= 23o26' 44,835"
EC(2000)
= 23o26' 21,409"
Het MC wordt als volgt berekend :
tan(MC)
= tan(RKMC) / cos(EC)
Het MC voor 1950:
De Sterretijd is 3 uur, dus RKMC is
gelijk aan 3 x 15 = 45 graden.
tan(RKMC)
= tangens(45) = 1.
cos(EC)
= 0,917 436 9
1
/ cos(EC) = 1,089 993 2
dit terugrekenen als tangens geeft :
MC
= 47,465 579 8 = 17o27' 56" Stier.
Het MC voor 2000:
RKMC is weer 45 graden.
tan(RKMC) is weer 1
cos(EC)
= 0, 917 482 1
1
/ cos(EC) = 1,089 939 5
dit terugrekenen als tangens geeft:
MC
= 47,464 174 1 = 17o27' 51" Stier.
U ziet dat dit een klein verschil geeft
in de positie van het MC, maar dit geldt ook voor alle andere
horoskoophuizen.
Doordat ik een belangrijk astronomisch
verschijnsel, nl. de nutatie nog
niet heb besproken, is de helling van de ecliptica niet helemaal perfect.
Invloeden van Zon, Maan en planeten geven elk nog een kleine 'duw' en
'trek' aan de aardas, zodat voor de ecliptica nog een maximaal verschil
van zo'n 10 boogseconden te verwachten is.
Het onderwerp nutatie is een afzonderlijk artikel waard, want het beÔnvloedt ook
de lengte van Zon, Maan, Draconis en ook de ST-berekening is hiervan
afhankelijk. Zonder de effecten van de nutatie mee te nemen, zal elke
berekening van de hemellichamen afwijkingen vertonen.
Door deze nutatie kan het verschil in
de huizenpositie nog eens een keer met 3" toenemen, dus een
totaalverschil van 8" veroorzaken en dat is toch wel de moeite waard.
De berekening van het MC heb ik nogal
summier opgesteld. Als u hierover meer wilt lezen, dan kan ik u aanraden
om Sagittarius 1980-nr.10 door te nemen. Hierin wordt de theoretische
berekening van de Placidus-huizen besproken.
De
invloed van de ecliptica op de declinaties van de horoskoophuizen.
De declinaties van de huizen, Draconis,
Pars Fortuna en Zon kunt u bepalen aan de hand van speciaal opgestelde
declinatietabellen, maar u kunt ze ook zelf berekenen. De genoemde
objecten hebben allemaal gemeen dat ze geen breedte hebben.
Daardoor kan de formule sterk vereenvoudigd worden. De formule voor de
declinatie luidt :
sin(decl)
= sin(lengte) x sin(EC)
Declinatie voor het MC van 1950:
Lengte
MC = 47,465 579 8.
sin(lengte)
= 0,736 871 3 [1]
sin(EC1950)
= 0,397 881 1 [2]
sin(decl)
= [1] x [2] = 0,293 187 2
Dit terugrekenen als sinus geeft:
Decl.
MC = 17,048 867 = 17o02'56"
N.
Declinatie
voor het MC van 2000:
Lengte MC = 47,464 174 1.
sin(lengte) = 0,736 854 7
[1]
sin(EC2000) =
0,397 776 9 [2]
sin(decl) = [1] x [2] =
0,293 103 8
Dit
terugrekenen als sinus geeft:
Decl. MC = 17,043 870 = 17o02'
38" N.
U ziet zelf dat het verschil tussen
beide declinaties zo'n 18" bedraagt. Dit kan eventueel ook weer meer
worden als u de nutatie in de
ecliptica zou verwerken.
De
allerlaatste ontwikkelingen.
Zoals ik in de eerste aflevering al
schreef, zijn naar aanleiding van de (1976) System of Astronomical
Constants nieuwe massa's voor de planeten bepaald. Dit naar aanleiding van
de meest recente observaties van de laatste 20 jaar. Deze nieuwe massa's
hebben ook weer gevolgen gehad voor de ecliptica formule.
Als u de oude formule nog even gebruikt
en uitrekent wat de ecliptica zal zijn voor J2000.0 (T=1), dan komt u uit
op :
EC = 23o26' 21,409".
Door de nieuwe constanten en massa's is
de ecliptica voor J2000.0 officieel vastgesteld op: 23o26'
21,448".
Het blijkt nl. dat de eerder bepaalde
afname per Juliaanse Eeuw van 46,845" in werkelijkheid iets minder
is.
Een nieuwe formule is uitgewerkt,, die
zowel tegemoet komt aan de ecliptica van 23o26' 21,448" op
J2000 als aan de eclipticawaarde van 23o27' 08,2584" op
J1900.
De meest recente formule voor de
ecliptica n.a.v. de (1976) System of Astronomical Constants luidt volgens
Lieske7 (epoch J2000.0):
|
EC = 23o26'
21,448"
- 46,815" T
+
0,001813".T3 |
De ecliptica voor de epoch J2000 is
uiteraard 23o26' 21,448". Rekent u de ecliptica uit voor
de oude epoch J1900, (dus T=-1 bezien vanuit de nieuwe standaard-epoch
J2000), dan krijgt u : EC = 23o26' 21,448" + 46,815"
- 0,00059" + 0,001813" = 23o27' 8,2605"
Het verschil tussen de berekende waarde
van 8,2605" voor J1900 en de vastgestelde waarde 8,2584" door
Newcomb in 1900 bedraagt slechts 0,0021"
en wij zullen ons hiermee tevreden moeten stellen.
De
volgende keer behandelen wij de berekening van de Draconis.
Literatuur:
i.
Th. v. Berkel, Sagittarius
(1983), 4, 26-27;
ii.
Th. v. Berkel, Sagittarius
(1985), 5, 38;
iii.
R.R. Newton, "The Authenticity of Ptolemy's Parallax Data", Quart. J. Astr.
Soc. (1973), 14, 367-388;
iv.
A. Wittmann, "The Obliquity of the Ecliptic", Astron. Astrophys. (1979), 73,
129-131;
v.
Explanatory Supplement to the Astronomical Ephemeris, Nautical
Almanac Office, 1977;
vi.
J. Ligteneigen, Sagittarius (1980), 10, 18-19;
vii.
Lieske et.al., "Expressions for the Precession Quantities", Astron. Astrophys.(1977),58,1-16.
_______________________________________________
Pagina voor het laatst bewerkt op / Page maintained on: 31/12/2015